原题链接：https://leetcode.cn/problems/longest-palindromic-substring/

难度：中

题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = “babad”

输出：“bab”

解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”

输出：“bb”

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

解题

思路描述

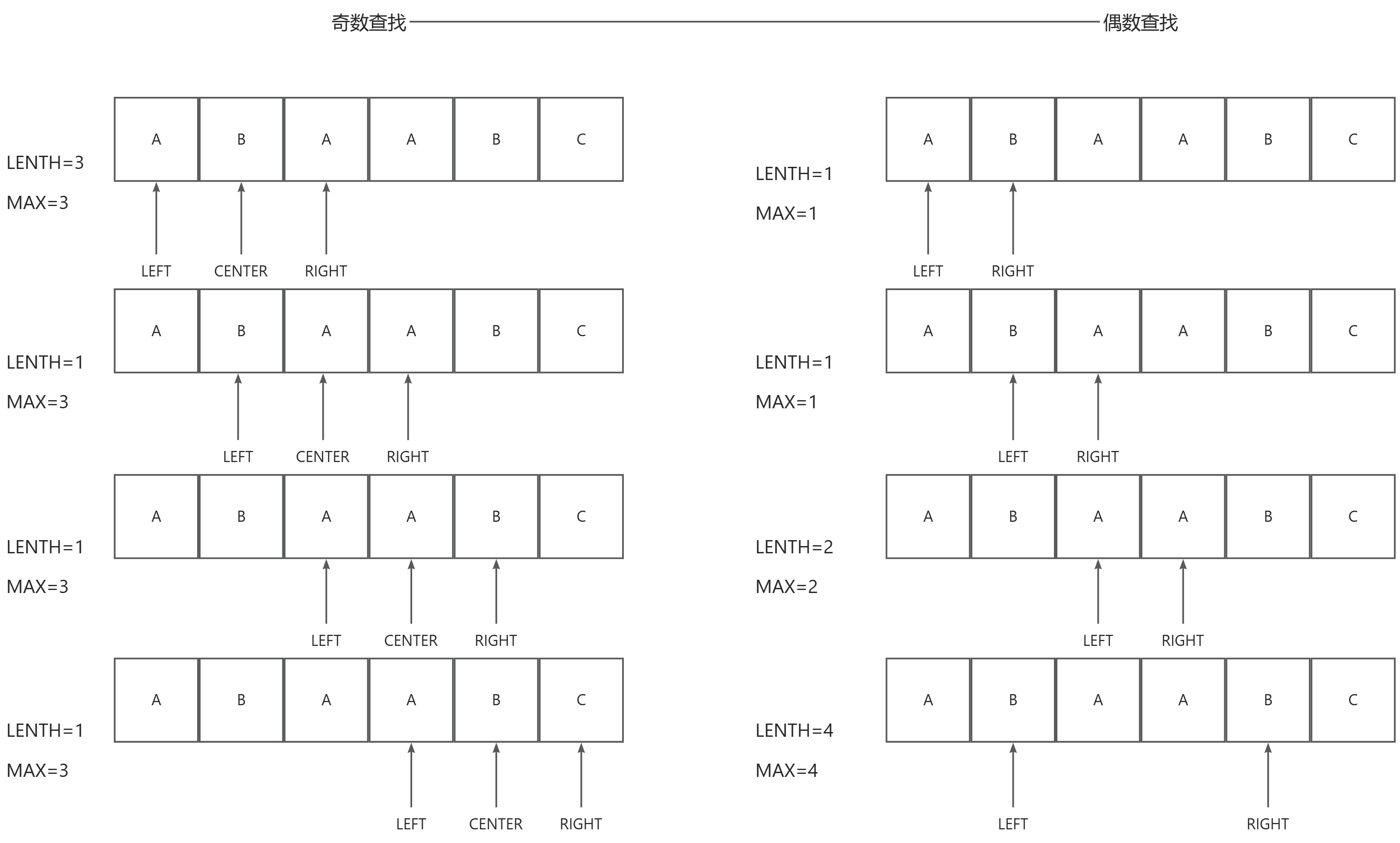
回文子串即对称位置的值相等，判断是否为回文子串，需要注意两种情况

• 字串长度为奇数
• 字串长度为偶数

先分析字串长度为奇数的情况

奇数时相对容易，由于字符串长度为一时一定回文，因此，过程如下：

1. 创建一个循环，控制CENTER从一端移向另一端
2. 使用两个指针LEFT和RIGHT，分别指向CENTER的两侧
3. 判断*LEFT和*RIGHT是否相等，并判断LEFT是否大于等于0，RIGHT要小于字符串长度-1

• • 如果相等，LEFT和RIGHT向两端扩展，并继续这一步的判断
  • 如果不相等，移动CENTER，重新调整LEFT和RIGHT的位置，开始新一轮的判断

1. 如果本轮判断结果是*LEFT和*RIGHT不相等，则统计此时回文子串的长度
2. 不能使用RIGHT-LEFT+1统计字符串长度，因为此时指针指向的值不相等，此方法求出的长度比实际长度多2，因此应该用RIGHT-LEFT-1统计字符串长度
3. 将每轮循环的结果与当前统计的最大值作比较
4. 当RIGHT-LEFT-1大于MAX时，将当前值赋值给MAX，并创建一个字符串，将当前字串赋值给该字符串

左图中的情况

1. 首先，CENTER指向第二个元素，LEFT和RIGHT分别在其左右
2. 判断*LEFT等于*RIGHT，指针向两侧移动，移动之后重复判断，不满足LEFT大于等于0的条件，循环终止，CENTER指向下一个位置，LENTH=3，MAX=3
3. 第二幅图中*LEFT不等于*RIGHT，CENTER后移，LENTH=1，MAX=3
4. 如此重复，最后LENTH=1，MAX=3；

字串长度为偶数时

步骤与奇数时类似，难在如何高效地同时处理奇偶两种情况。

还应注意的是，最后的返回值类型要求是字符串：

• 对于字符串长度为奇数这种情况，容易理解：(LEFT+RIGHT)/2=CENTER，RIGHT-LEFT-1=MAX根据这两个方程即可确定截取的原字符串位置
• 对于字符串长度为偶数这种情况，需要设初始状态的LEFT=CENTER，RIGHT=CENTER+1，同样，通过解方程组，求出需要截取的字符串范围

敲代码

如果文字思路太抽象、看不懂，就多看几遍下面的代码

对于上面两种情况，可以发现，扩展部分的原理是相同的，我们可以将这一部分单独封装，重复使用

class Solution { public:  int search(const string& s, int left, int right)  {  while (left >= 0 && right < s.size() && s[left] == s[right])  {  left--;  right++;  }  return right - left - 1;  }  string longestPalindrome(string s) {  int mx(1);  string result = s.substr(0, 1);  for (int i = 0; i < s.size(); i++)  {  int sg = search(s, i - 1, i + 1);  int db = search(s, i, i + 1);  if (max(sg, db) > mx)  {  mx = max(sg, db);  result = s.substr(i - (mx - 1) / 2, mx);  }  }  return result;  } };

运行效果

141 / 141 个通过测试用例

执行用时: 16 ms

内存消耗: 9.1 MB

加break及时跳出

当目前的最长回文子串长度超过剩余字符串长度的两倍时，在循环移动已无意义，因为接下来的子串长度一定不会超过目前的长度

代码实现

class Solution { public:  int search(const string& s, int left, int right)  {  while (left >= 0 && right < s.size() && s[left] == s[right])  {  left--;  right++;  }  return right - left - 1;  }  string longestPalindrome(string s) {  int mx(1);  string result = s.substr(0, 1);  for (int i = 0; i < s.size() - mx / 2; i++)  {  int sg = search(s, i - 1, i + 1);  int db = search(s, i, i + 1);  if (max(sg, db) > mx)  {  mx = max(sg, db);  result = s.substr(i - (mx - 1) / 2, mx);  }  }  return result;  } };

运行效果

执行用时: 4 ms

内存消耗: 9.1 MB

总结

这个题一共有如下几个重点：

• 子串长度分别为奇数和偶数的情况
• 返回值是字符串而非整型
• 及时跳出

对于第一点，举例假设的方法寻找规律

第二点，每轮循环求得最大值后，保留当前的最长字串

第三点，模拟一下