< 返回新闻公共列表
树的进化
发布时间:2023-06-26 13:59:54
- 线性查找(效率低)->二分查找->二叉查找树(易退化成链表)->AVL平衡二叉树(数据变化频繁更新节点)->红黑树(在平衡之中的取舍,不追求绝对的平衡)
- AVL树:任何节点两个子树的高度差绝对值小于等于1;AVL树所希望的是一种绝对的平衡,当数据发生变动时,AVL树会进行旋转处理。而我们需要考虑的则是对于AVL树绝对平衡所需要的代价
- AVL树中最耗费时间的实际上是数据发生改变后的,重新构造一颗平衡树。
- 红黑树舍弃了AVL树的绝对平衡,更多的是一种折中的方式
- 节点非黑即红
- 根节点必为黑
- 没有连续的红色节点
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点
- 设一个节点存在k个关键字,则必然存在k+1个孩子
- B树的数据每个节点都存在
- 每个节点的元素按照值域划分,从大到小
- B树如下:
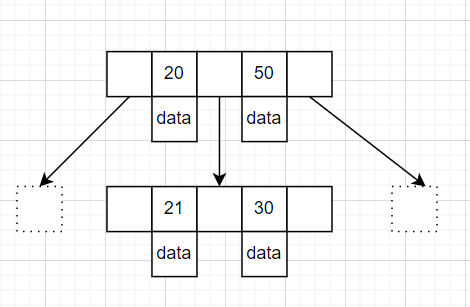
- 设一个节点存在k个关键字,则必然存在k个子节点
- B+树仅在叶子节点存放数据
- B+树的叶子节点包含了指向下一个节点的指针
- B+树如下:
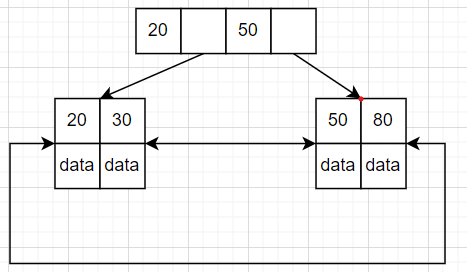
- B+Tree不需要做中序遍历,因此不需要回查其余的节点,只需要遍历叶子节点,因此减少了回查节点的I/O次数
- B+Tree中间节点不包含数据,所以B+Tree在同样页面下所加载的索引会更多,减少了缺页中断的次数以及I/O的次数

