数值分析算法 MATLAB 实践 线性方程组迭代法

Jacobi迭代法

雅可比迭代法保证收敛的条件是矩阵A(Ax=b)为严格的行对角占优矩阵，对于每一行，对角线上的元素之绝对值大于其余元素绝对值的和。需要说明的是：即使不满足此条件，雅可比法有时仍可以收敛。

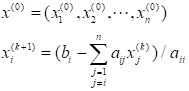
%% 雅可比迭代法 [x,k,index] = Jacobimethod(A,b,ep)% A为方程组的系数矩阵；% b为方程组的右端项;% ep为精度要求，缺省值为1e-5;% it_max为最大迭代次数，缺省值为100;% x为方程组的解;% k为迭代次数;% index为指标变量，index=0表示迭代失败，index=1表示收敛到指定要求
A = [10 3 1; 2 -10 3 ;1 3 10];b = [14 -5 14 ]'; %b = [14; -5; 14 ];eps = 0.005;[x_0,k0_cnt,index] = Jacobimethod(A,b,eps);disp('迭代次数:k0_cnt=')disp(k0_cnt)disp(['方程组的解：x_0 = '])disp(x_0)%% 求线性方程组的Jacobi迭代法，调用格式为[x, k] = JacobiFunc(A,b,x0,eps,it_max)%  其中, A 为线性方程组的系数矩阵，b 为常数项，eps 为精度要求，默认为1e-6,x0迭代初始值%  it_max 为最大迭代次数，默认为1000%  x 为线性方程组的解，k迭代次数
x0=[0,0,0]';%[x1;x2;x3]列向量
it_max = 1000;eps=1e-6;[x1, k1_cnt] = JacobiFunc(A,b,x0,eps,it_max);disp('迭代次数:k1_cnt=');disp(k1_cnt)disp(['方程组的解：x1 = ']);disp(x1)

 %% [x,k]=JacobiFunmethod(A,b,x0,N,emg)
 % A:线性方程组左端矩阵，b:线性方程组右端向量，x0:迭代初值 % N:迭代次数上界，若迭代次数大于n，则迭代失败， emg:精度指标 % k:迭代次数， % x:用迭代法求得的线性方程组的近似解
x0=[0,0,0]';%[x1;x2;x3]列向量
it_max = 1000;eps=1e-6;[x2,k2_cnt]=JacobiFunmethod(A,b,x0,it_max,eps);disp('迭代次数:k2_cnt=');disp(k2_cnt)disp(['方程组的解：x2 = ']);disp(x2)

function [x,k] = JacobiFunc(A,b,x0,eps,it_max)
%  求线性方程组的Jacobi迭代法，调用格式为[x, k] = JacobiFunc(A,b,x0,eps,it_max)
%  其中, A 为线性方程组的系数矩阵，b 为常数项，eps 为精度要求，默认为1e-6,x0迭代初始值
%  it_max 为最大迭代次数，默认为200
%  x 为线性方程组的解，k迭代次数
  if nargin == 3
      eps = 1.0e-6;
      M = 200;
  elseif nargin=eps
      x0 = x;
      x = B*x0+f;
      k = k+1;
      if(k>=M)
          disp('Warning:迭代次数太多,可能不收敛!');
          return;
      end
  end
end

function [ x,k,index]=Jacobimethod(A,b,ep,it_max)
% 求线性方程组的雅可比迭代法，其中，
% A为方程组的系数矩阵；
% b为方程组的右端项;
% ep为精度要求，缺省值为1e-5;
% it_max为最大迭代次数，缺省值为100;
% x为方程组的解;
% k为迭代次数;
% index为指标变量，index=0表示迭代失败，index=1表示收敛到指定要求,
    [n,m] = size(A);nb = length(b);
%当方程组行与列的维数不相等时，停止计算，并输出出错信息。
    if n ~=m
            error('The rows and columns of matrix A must be equal! ');
            return;
    end
    % 当方程组与右端项的维数不匹配时，停止计算，并输出出错信息。
    if m~=nb
            error ('The columns of A must be equal the length of b! ');
            return;
    end

    if nargin<4
        it_max =100;
    end
    if nargin<3 
        ep = 1e-5;
    end

    k=0;x = zeros (n,1);y=zeros (n,1);index=1;
    while 1
        for i=1 :n
                y(i) =b(i) ;
                for j=1:n
                    if j~=i
                            y(i) =y(i) -A(i,j)*x(j);
                    end
                end
       if abs(A(i,i))<1e-10  &&k==it_max       % abs绝对值函数
                    index =0 ;return;
                end
                y(i) =y(i)/A(i,i);
        end
        k = k +1;
        if norm(y-x,inf) <ep
            break;
        end
        x = y;
end

function [x,k]=JacobiFunmethod(A,b,x0,N,emg)
 % A:线性方程组左端矩阵，b:线性方程组右端向量，x0:迭代初值
 % N:迭代次数上界，若迭代次数大于n，则迭代失败， emg:精度指标
 % k:迭代次数，
 % x:用迭代法求得的线性方程组的近似解
     n=length(A);      
     x=zeros(n,1); %设置变量
     X=zeros(n,1); % X
     x=x0; k=0; 
     r=max(abs(b-A*x));
     while (r>emg)          % 迭代循环过程
       for i=1:n
           sum=0;
           for j=1:n
                if i~=j
                 sum=sum+A(i,j)*x(j);
                end
           end
           X(i)=(b(i)-sum)/A(i,i);
       end
       r=max(abs(X-x)); 
       x=X; 
       k=k+1;
       if k>N
          disp('迭代失败，返回');
          return;
       end
end