
function [x,y] = euler(fun,a,b,h,y0) %一阶常微分方程的一般表达式的右端函数:fun % 显示欧拉格式 % f是带求函数的一阶导形式 % a,b分别是自变量取值上下限 % y0 是初始条件y(0) % h是步长 s = (b - a) / h; % 求步数 X = zeros(1, s+1); Y = zeros(1, s+1); X = a:h:b; Y(1) = y0; for k = 1:s Y(k+1) = Y(k) + h * fun(X(k), Y(k)) end x = X'; y = Y'; end
%% euler求解微分方程
% dfun1 = y^2-y^3;
[x, y] = euler(@dfun1, 0,5,0.01,0.1);
% dfun1 = y;
% [x, y] = euler(@dfun1, 0,1,0.1,1);
figure
plot(x, y);
title('显示欧拉格式');
%% 微分方程
function dfun1 = dfun1(t,y)
dfun1 = y^2-y^3;
%dfun1 = y;
endfunction[x,y]=imp_euler(func,a_start,b_end,h_step,y0) %一阶常微分方程的一般表达式的右端函数:fun % 显示欧拉格式 % func是带求函数的一阶导形式 % a_start,b_end分别是自变量取值上下限 % y0是初始条件y(0) % h_step是步长 x = a_start : h_step : b_end; N = length(x); y = zeros(1, N); y(1) = y0; for i = 2:N % 显式 Euler 作为初始值迭代计算 yi_0 = y(i-1) + h_step * func(x(i-1), y(i-1)); yi_1 = y(i - 1) + h_step * func(x(i), yi_0); while abs(yi_1 - yi_0) > 1e-6 yi_0 = yi_1; yi_1 = y(i - 1) + h_step * func(x(i), yi_0); end y(i) = yi_1; end
function[x,y]=improve_euler(func,a_start,b_end,h_step,y0) %一阶常微分方程的一般表达式的右端函数:fun % 显示欧拉格式 % func是带求函数的一阶导形式 % a_start,b_end分别是自变量取值上下限 % y0是初始条件y(0) % h_step是步长 x = a_start : h_step : b_end; N = length(x); y = zeros(1, N); y(1) = y0; for i = 2:N yp = y(i-1) + h_step * func(x(i-1), y(i-1)); yq = y(i-1) + h_step * func(x(i), yp); y(i) = 0.5 * (yp + yq); end
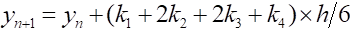
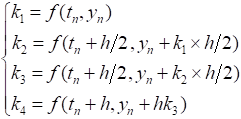
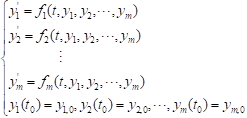
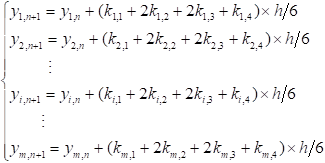
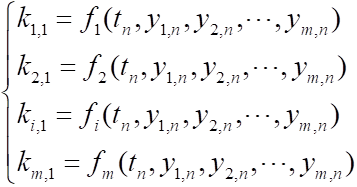
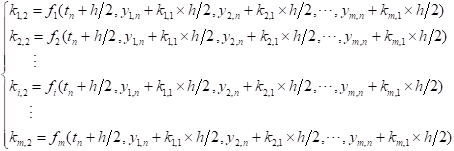
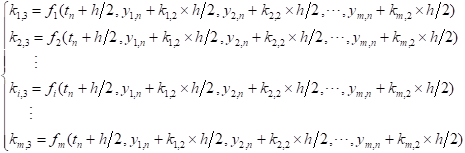
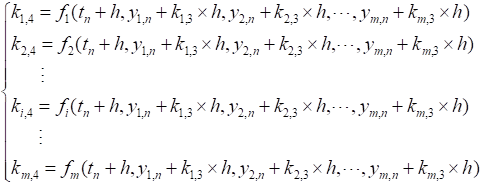

% 单变量龙格库塔Runge_kutta 经典法 %一阶常微分方程的一般表达式的右端函数:func % func是带求函数的一阶导形式 % a_start,b_end分别是自变量取值上下限 % y0是初始条件y(0) % h_step是步长 function[x,y]=Runge_kutta(func,a_start,b_end,h_step,y0) x = a_start : h_step : b_end; N = length(x); y = zeros(1, N); y(1) = y0; for i = 2:N k1 = func(x(i-1), y(i-1)); k2 = func(x(i-1) + h_step/2, y(i-1) + h_step/2*k1); k3 = func(x(i-1) + h_step/2, y(i-1) + h_step/2*k2); k4 = func(x(i-1) + h_step, y(i-1) + h_step*k3); y(i) = y(i-1) + h_step/6*(k1 + 2*k2 + 2*k3 + k4); end
function[x,y]=Runge_kutta45(dyfunc,xspan,y0,h_step) % 多变量龙格库塔Runge_kutta45 % h_step是步长常选取为0.01; % ufunc是函数名; % x0是初始时间值; % y0是初始化值; % n 是迭代步数; x = xspan(1):h_step:xspan(2); y = zeros(length(y0),length(x)); y(:,1) = y0(:); %循环迭代数值求解部分 for n=1 : (length(x)-1) k1=feval(dyfunc, x(n),y(:,n)); k2=feval(dyfunc, x(n)+h_step/2,y(:,n)+h_step/2*k1); k3=feval(dyfunc, x(n)+h_step/2,y(:,n)+h_step/2*k2); k4=feval(dyfunc, x(n+1),y(:,n)+h_step*k3); y(:,n+1)=y(:,n)+h_step*(k1+2*k2+2*k3+k4)/6; %按照4阶多变量龙格库塔方法进行数值求解 end end
clc;
clear all;
y0=[0,2,9];%初值
xspan = [0,200];%求解区间
h_step = 0.001;%ode45是变步长的算法
[x,y] = Runge_kutta45(@lorenz_diff,xspan,y0,h_step);
figure(1);
plot3(y(1,:),y(2,:),y(3,:),'.');title("x-y-z");
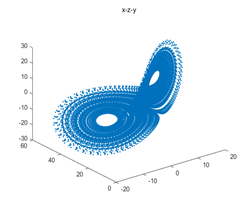
figure(2);
plot3(y(1,:),y(3,:),y(2,:),'.');title("x-z-y");
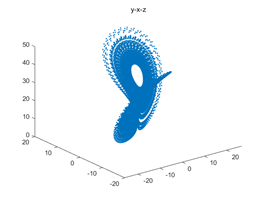
figure(3);
plot3(y(2,:),y(1,:),y(3,:),'.');title("y-x-z");
function dydt = lorenz_diff(t,y)
%{
x-->y(1),y-->y(2),z-->y(3)
%}
dydt = [ 10*(y(2)-y(1));
-y(1)*y(3)+30*y(1)-y(2)
y(1)*y(2)-8/3*y(3)];
end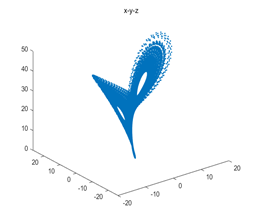
[t, Xt] = ode45(odefun, tspan, X0) odefun是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名 tspan是区间 [t0 tfinal] 或者一系列散点[t0,t1,…,tf] X0是初始值向量 t返回列向量的时间点 Xt返回对应T的求解列向量
Lorenz系统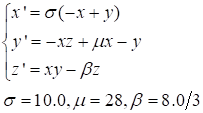
function dydt = lorenz_diff(t,y)
%{
x-->y(1),y-->y(2),z-->y(3)
%}
dydt = [ 10*(y(2)-y(1));
-y(1)*y(3)+30*y(1)-y(2)
y(1)*y(2)-8/3*y(3)];
end
clc;
y0 = [0,2,9];
[t,y] = ode45('lorenz_diff',[0,200],y0);
%% 调用ode45绘制Lorenz系统 2D
figure(1);
plot(y(:,1),y(:,3),'.');
xlabel('x');ylabel('z');title("x-z");
figure(2);
plot(y(:,1),y(:,2),'.');
xlabel('x');ylabel('y');title("x-y");
figure(3);
plot(y(:,2),y(:,3),'.');
ylabel('y');zlabel('z');title("y-z");
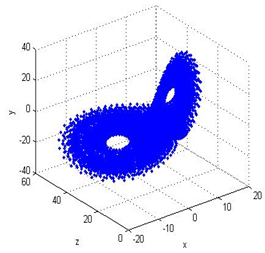
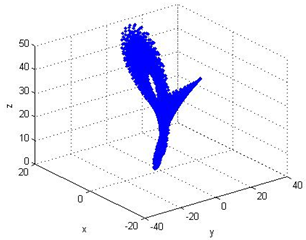
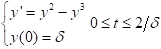
%% 火焰传播数学模型求解
clc;
clear all;
delta=0.01;
f=@(t,y)y^2-y^3;
opts=odeset('Reltol',1.e-4);
[t1,y1]=ode45(f,[0 2/delta], delta, opts);
figure(1)
plot(t1,y1,'-','Marker','.');
title('数值解曲线');
ylabel('y'); xlabel('t');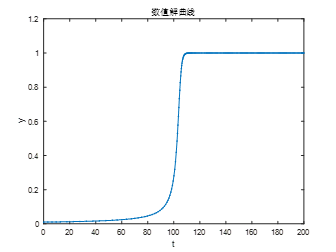
Copyright © 2023 leiyu.cn. All Rights Reserved. 磊宇云计算 版权所有 许可证编号:B1-20233142/B2-20230630 山东磊宇云计算有限公司 鲁ICP备2020045424号
磊宇云计算致力于以最 “绿色节能” 的方式,让每一位上云的客户成为全球绿色节能和降低碳排放的贡献者