统计分析 -- 聚类算法模型

距离分析

数据标准化

欧氏距离与量纲有关，因此，有时需要对数据进行预处理，
如标准化等。
在MATLAB中的命令是zscore，调用格式

Z = zscore(X)
输入X表示N行p列的原始观测矩阵，行为个体，列为指标。

输出Z为X的标准化矩阵:
Z = (X–ones(N,1)*mean(X)) ./(ones(N,1)* std(X))，

mean(X)为行向量，表示各个指标的均值估计，
std（X）表示指标的标准差估计。./表示对应元素相除，
ones(N,1)表示元素全为1的行向量，向量的长度为N。

K-means聚类

K-means聚类的算法流程：

1. 指定需要划分的簇的个数K值（类的个数）
2. 随机地选择K个数据对象作为初始的聚类中心（不一定要是我们的样本点）
3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中；
4. 调整新类并且重新计算出新类的中心；
5. 循环步骤3和4，看中心是否收敛（不变）如果敛或达到迭代次数则停止循环；
6. 结束。

K-means聚类特点

K-means++聚类算法

SPSS软件使用

code

%% 
% K-means 算法MATLAB实现
%-------------------------------------------------------------
%{
利用Matlab软件中的命令: kmeans,可以实现k-means聚类
对于要处理的数据 构造矩阵，矩阵X的每一行为每个个体的实际数据，每一列都是不同的指标
如果提供的数据不是按照规范模式，需要进行矩阵转置
x=y';     %矩阵x的行为个体，列为指标  
[a,b]=kmeans(x,2)　　%分为2类，输出:  a为聚类的结果，b为聚类重心, 每一行表示一个类的重心
使用kmeans进行处理 
%}
%% 数据准备和初始化
clc
clear
load kdata.mat


[a,b]=kmeans(x,3);  %%分为3类输出
x1=x(find(a==1),:)   %提取第1类里的样品
x2=x(find(a==2),:)   %提取第2类里的样品
x3=x(find(a==3),:)   %提取第3类里的样品
sd1=std(x1)
sd2=std(x2)　 
sd3=std(x3)　 % 分别计算第1类和第2类第3类的标准差
plot(x(a==1,1),x(a==1,2),'r.',x(a==2,1),x(a==2,2),'b.',x(a==3,1),x(a==3,2),'g.','MarkerSize',10)  %作出聚类的散点图
title('k-means聚类分析散点图');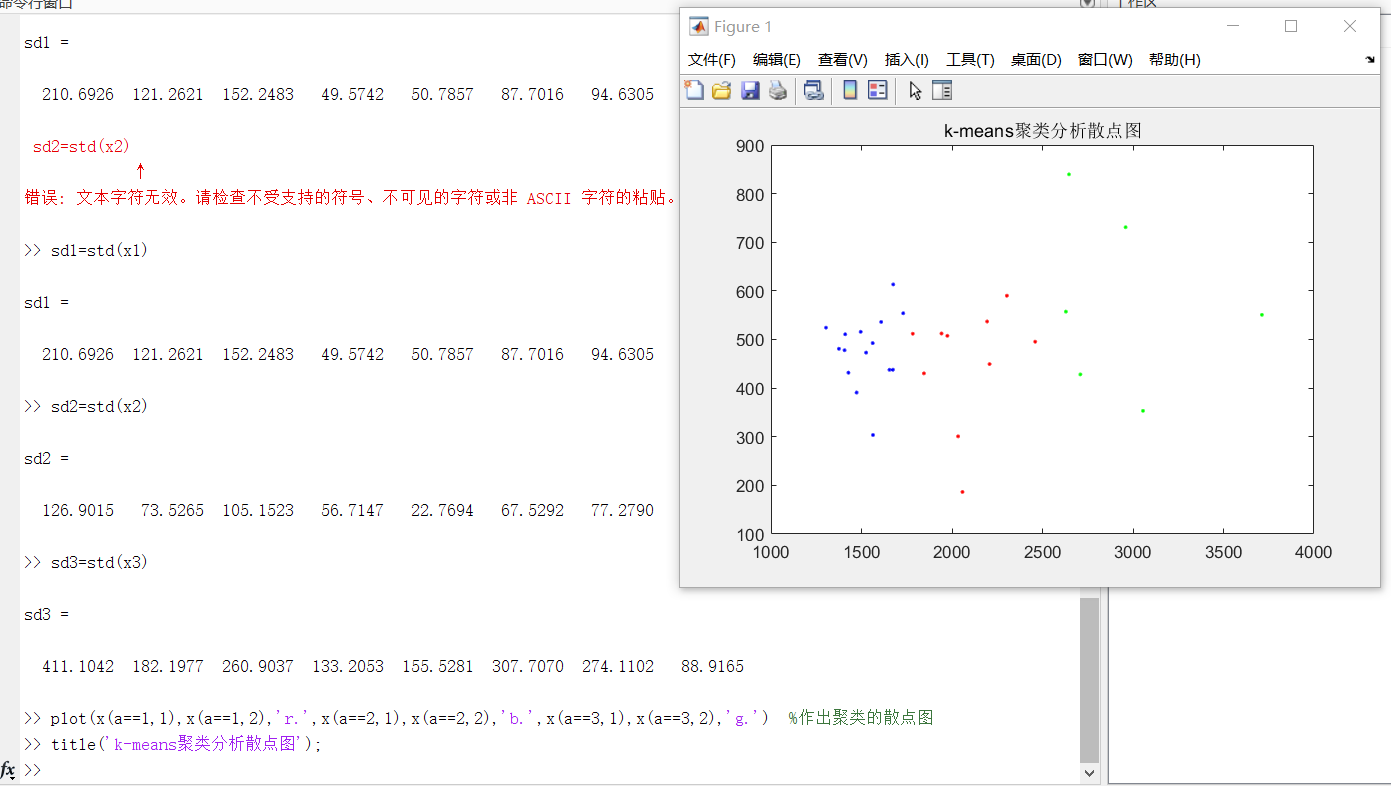

聚类分析--谱系分析

研究聚类的MATLAB实现，实现步骤大致如下：

1. 输入数据矩阵，注意行与列的实际意义；
2. 计算各样品之间的距离（行？列？）
   欧氏距离：d=pdist(A) % 注意计算A中各行之间的距离；
   绝对距离：d= pdist(A,'cityblock');
   明氏距离：d=pdist(A,'minkowski',r); % r要填上具体的实数；
   方差加权距离：d= pdist(A,'seuclid');
   马氏距离：d= pdist(A,'mahal');
   注意：以上命令输出的结果是一个行向量
3. 选择不同的类间距离进行聚类
4. 作出谱系聚类图
5. 根据分类数目，输出聚类结果

试利用调查资料对16个地区进行聚类分析。

下表是我国16个地区农民1982年支出情况的抽样调查的汇总资料，每个地区都调查了反映每人平均生活消费支出情况的六个指标。

谱系聚类图

a=load('ho2.txt');%导入数据

d1=pdist(a);% 此时计算出各行之间的欧氏距离，

z1=linkage(d1);

z2=linkage(d1,'complete');

z3=linkage(d1,'average');

z4=linkage(d1,'centroid');

z5=linkage(d1,'ward');

R=[cophenet(z1,d1),cophenet(z2,d1),cophenet(z3,d1),cophenet(z4,d1),cophenet(z5,d1)]

H= dendrogram(z3)

T=cluster(z3,4)  %cluster 创建聚类，并作出谱系图

set(get(gca, 'Title'), 'String', '聚类分析-谱系聚类图');

k-means聚类分析散点图

[a,b]=kmeans(x,4);  %%分为4类输出
x1=x(find(a==1),:)   %提取第1类里的样品
x2=x(find(a==2),:)   %提取第2类里的样品
x3=x(find(a==3),:)   %提取第3类里的样品
x4=x(find(a==4),:)   %提取第3类里的样品
sd1=std(x1)
sd2=std(x2)　 
sd3=std(x3)　 % 分别计算第1类和第2类第3类的标准差
sd4=std(x4)　 % 分别计算第1类和第2类第3类的标准差
plot(x(a==1,1),x(a==1,2),'r.',x(a==2,1),x(a==2,2),'b.',x(a==3,1),x(a==3,2),'g.',x(a==4,1),x(a==4,2),'y.','MarkerSize',15)  %作出聚类的散点图
title('k-means聚类分析散点图');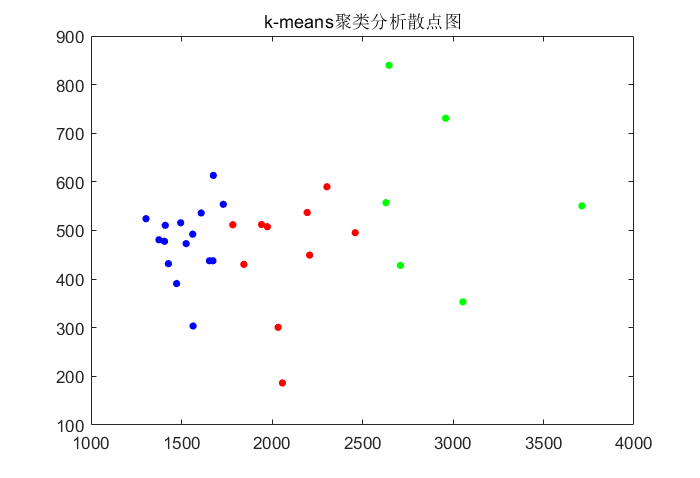

linkage函数
调用格式：Z=linkage(Y,‘method’)
输入值说明：Y为pdist函数返回的M*(M-1)/2个元素的行向量，用‘method’参数指定的算法计算系统聚类树。
method：可取值如下：
‘single’：最短距离法（默认）；
‘complete’：最长距离法；
‘average’：未加权平均距离法；
‘weighted’： 加权平均法；
‘centroid’：质心距离法；
‘median’：加权质心距离法；
‘ward’：内平方距离法（最小方差算法）
返回值说明：Z为一个包含聚类树信息的（m-1）×3的矩阵，其中前两列为索引标识，表示哪两个序号的样本可以聚为同一类，第三列为这两个样本之间的距离。另外，除了M个样本以外，对于每次新产生的类，依次用M+1、M+2、…来标识