统计分析 -- 判别分析算法模型

模型概括

MATLAB中有一个命令:
d= mahal(Y,X) 计算X矩阵每一个点（行）至Y矩阵中每一个点（行）的马氏距离。
其中: Y的列数必须等于X的列数，但它们的行数可以不同。X的行数必须大于列数。输出d:  d是距离向量。

距离判别分析

两总体的距离判别分析

例题

1.总体协方差矩阵相等

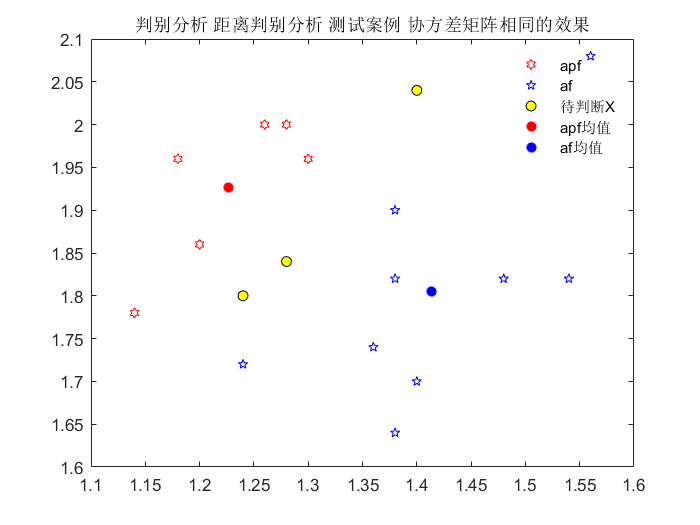
apf =  [1.14,1.78;1.18,1.96;1.20,1.86;1.26,2.;1.28,2;1.30,1.96];
af  = [1.24,1.72;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08];
x = [1.24,1.8;1.28,1.84; 1.4,2.04]; 
%输入原始待判别数据
m1 = mean( apf ); m2 = mean( af ); % 计算样本均值
s1 =  cov(apf); s2 =  cov(af); %  协方差矩阵
%计算总体的协方差矩阵
s = ((length(apf)-1)*s1+(length(af)-1)*s2)/(length(af)+length(apf)-2);
for i=1:length(x)
    %计算判别函数值
    W(i)=(x(i,:)-1/2*(m1+m2))* inv(s)*(m1-m2)';
end   
disp(['判别函数值:',num2str(W)])


plot(apf(:,1),apf(:,2),'rh');
hold on
plot(af(:,1),af(:,2),'bp');
plot(x(:,1),x(:,2),'ko','MarkerFaceColor','y');
apfm  = mean(apf);


plot( apfm (1), apfm(2),'r*','LineWidth',2);
afm = mean(af);
plot( afm (1), afm(2),'b*','LineWidth',2)
legend('apf','af','待判断X','apf均值','af均值')
legend('boxoff')
title('判别分析 距离判别分析 测试案例 协方差矩阵相同的效果')

2.总体协方差矩阵不相等

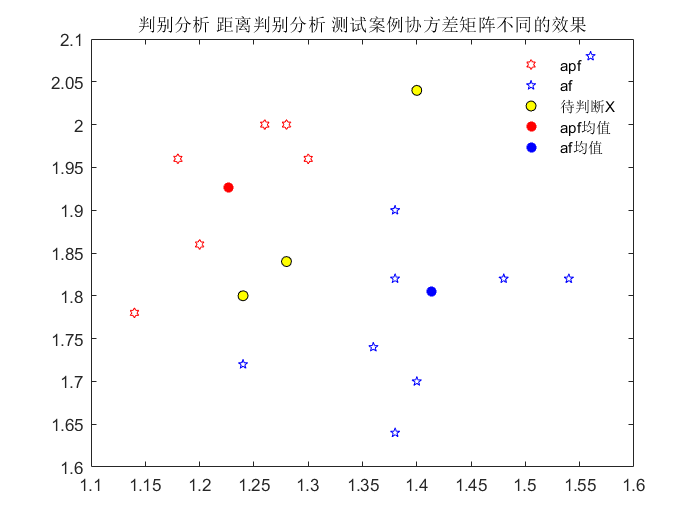
apf =  [1.14,1.78;1.18,1.96;1.20,1.86;1.26,2.;1.28,2;1.30,1.96];
af  = [1.24,1.72;1.36,1.74;1.38,1.64;1.38,1.82;1.38,1.90;1.40,1.70;1.48,1.82;1.54,1.82;1.56,2.08];
x = [1.24,1.8;1.28,1.84; 1.4,2.04]; 
W = mahal(x,apf)-mahal(x,af) %  计算判别函数


plot(apf(:,1),apf(:,2),'rh');
hold on
plot(af(:,1),af(:,2),'bp');
plot(x(:,1),x(:,2),'ko','MarkerFaceColor','y');
apfm  = mean(apf);


plot( apfm (1), apfm(2),'r*','LineWidth',2);
afm = mean(af);
plot( afm (1), afm(2),'b*','LineWidth',2)
legend('apf','af','待判断X','apf均值','af均值')
legend('boxoff')
title('判别分析 距离判别分析 测试案例 协方差矩阵不同的效果')

两种情况的区别

p=2; alpha  = 0.05;
Q01 = (n1-1)*(log(det(s))-log(det(s1))-p+trace(inv(s)*s1));
Q02 = (n2-1)*(log(det(s))-log(det(s2))-p+trace(inv(s)*s2));
lamda  = chi2inv(1-alpha,3);
if Q01<lamda  && Q02<lamda
disp(' 两总体协方差矩阵相同) .')
end