题目描述

平面直角坐标系中有一个点 CC 和一条直线 ABAB ,求点 CC 和直线 ABAB 的位置关系。

输入描述

第一行输入一个 TT ,代表测试数据量

每组测试数据输入有三行，每行一个实数坐标 (x, y)(x,y) 分别代表 A, B, CA,B,C 三个点。

1≤T≤10^3,−10^5≤x,y≤10^5。

输出描述

如果点 C 在直线 AB 上， 输出IN ， 如果点 C 在直线 AB 左侧，输出L， 如果点 C 在直线 AB 右侧输出R。

样例输入

样例输出

思路

我们首先介绍一个概念：叉积

叉积是两个矢量模的乘积再乘夹角正弦，经过推导可以发现两个向量A(x1,y1),B(x2,y2)的叉积为：

                                               x1∗y2−x2∗y1

在本题中我们输入三个点的坐标，在函数中直接计算向量CA，CB的值，再带入到叉积的计算中，算出叉积,这个函数实际上求的是CA*CB=|CA||CB|sinθ

1. def Cross(A,B,C): 2. return (A[0]-C[0])*(B[1]-C[1])-(B[0]-C[0])*(A[1]-C[1])

我们注意Cross的正负是有特殊含义的。如下图，Multi即为Cross,以p0为参考点，下图为向量p0p1和p0p2的叉积。如果Cross大于0，则p0p2在p0p1的逆时针方向，p0在p1p2的左边。反之，如果Cross小于0，则p0p2在p0p1的顺时针方向，p0在p1p2的右边。特殊的，当Cross等于0，p1、p2、p0三点共线。

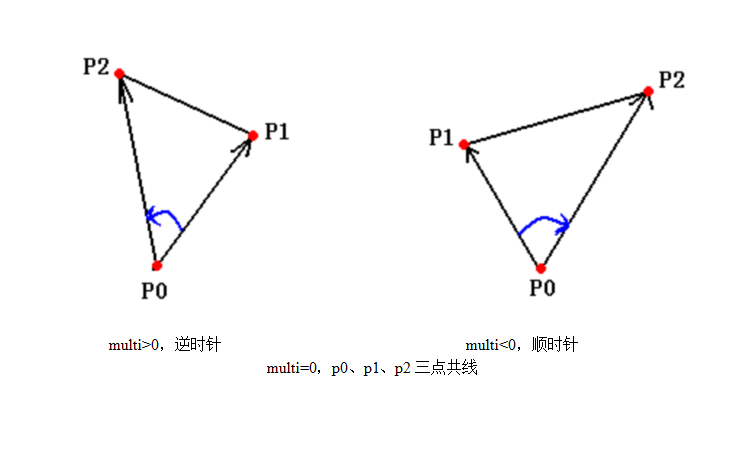
原理：A*B= |A|*|B|sinθ，其中这个角度可以想象为平面中有一坐标，它的值就是角P2P0x-角P1P0x的值。而我们题目中的要求的方向是A->B，即上图中P1->P2，所以当Cross>0,说明c在AB左边，<0,说明在右边。

代码

1. def Cross(A,B,C): 2. return (A[0]-C[0])*(B[1]-C[1])-(B[0]-C[0])*(A[1]-C[1]) 3. 4. def area(p1,p2,p3): 5. s=Cross(p1, p2, p3) 6. if s>0: 7. print("L") 8. elif s<0: 9. print("R") 10. else: 11. print("IN") 12. 13. t=int(input()) 14. for i in range(t): 15. a=tuple(map(float,input().split())) 16. b=tuple(map(float,input().split())) 17. c=tuple(map(float,input().split())) 18. area(a, b, c)