冒泡排序

依次比较相邻的两个元素，将比较小的数放在前面，比较大的数放在后面，直到所有元素排列完。

最容易理解的版本

对一个数组的n个整型数据进行n趟排序，每趟排序都尝试将较大值放到数组右侧。
每趟排序比较两个相邻的数据，由于n个数据有n-1个间隔，所以每趟需要比较n-1次。
代码如下：

Java

import java.util.Arrays;public class Main { public static void main(String[] args) { int[] ints = { 5, 2, 4, 3};//比较n趟for (int i = 0; i < ints.length; i++) { //每趟比较n-1次for (int m = 0; m < ints.length - 1; m++) { //将较大值置于数组右侧if (ints[m] > ints[m + 1]) { int tmp = ints[m];ints[m] = ints[m + 1];ints[m + 1] = tmp;}}}//检验结果System.out.println(Arrays.toString(ints));}}

C/C++

#includeint  main() { int ints[] = {  5,2,4,3 };//比较n趟for (int i = 0; i < sizeof(ints) / sizeof(ints[0]); i++) { //每趟比较n-1次for (int m = 0; m < sizeof(ints) / sizeof(ints[0]) - 1; m++) { ////将较大值置于数组右侧if (ints[m] > ints[m + 1]) { int tmp = ints[m];ints[m] = ints[m + 1];ints[m + 1] = tmp;}}}//检验结果for (int i = 0; i < sizeof(ints) / sizeof(ints[0]); i++) { printf("%d ", ints[i]);}}

进一步优化

上述代码存在优化空间：
在第一趟排序结束后，数组最右端已是当前的最大值5。剩余元素均小于5，后续排序无需再与5进行比较。
在第二趟排序结束后，数组最右侧是4,5，剩余元素均小于4,5，后续排序无需再对4,5进行比较。
即对于内层循环：

• 在第i趟排序中，只需要比较n-i次（i从1开始）。
• 如果外层循环是从0开始计数的，那么需要每轮需要比较n-1-i次。

对于外层循环，在执行第n-1趟排序时，内层循环只比较了第1个元素和第2个元素。
此时已经排列完成，不需要再执行下一趟排序。
即对于外层循环：

• 只需要排序n-1趟。
• 对于给定的数组，n-1的结果也是确定的。因此无论外层循环的计数器从几开始，需要比较的次数都是n-1。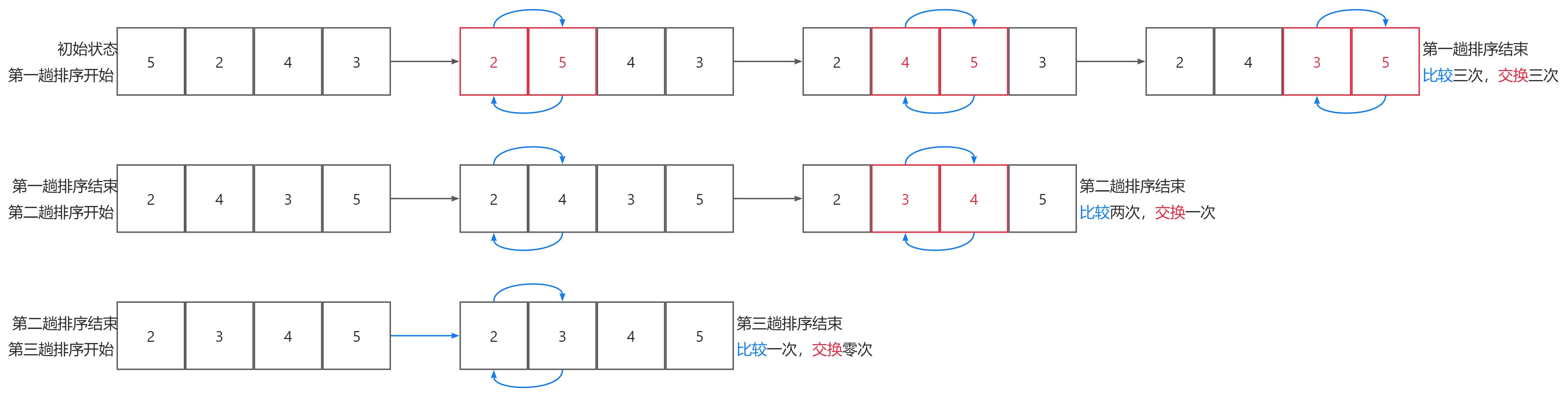

上面的例子比较简单，还有一种情况存在优化空间：在第n-1趟排序执行之前就已经排序完成。
这种情况的特征是：在某一趟比较之后，没有发生元素交换。
我们可以：

1. 定义一个标记flag并初始化为1。
2. 在每趟比较开始前，通过flag检查是否发生元素交换。
3. 在每趟比较开始时，将flag置为0。
4. 当发生元素交换时，将flag置为1。

在第2步中，如果flag值为1，则表明发生交换，继续下一步。
如果flag值为0，则表明没有发生交换，即已经排序完成，结束即可。

• flag初始值为1，可以正常进入第一趟排序。

• Java中Boolean类型不能赋值为1或0，将对应的1和0改为true和false即可。

  总结

• 外层循环控制轮数，总共执行n-1轮。

• 内层循环控制每轮的比较次数，第i轮比较n-i次（i从1开始）。
• 通过标记flag判断是否已经排序完成。

  C/C++

#includeint  main() { int ints[] = {  5,2,4,3 };//标记完成状态char flag = 1;//比较n-1趟for (int i = 0; i < sizeof(ints) / sizeof(ints[0]) - 1 && flag; i++) { //将标记置为0flag = 0;//计数器从0开始，每趟比较n-1-i次for (int m = 0; m < sizeof(ints) / sizeof(ints[0]) - 1 - i; m++) { //将较大值置于数组右侧if (ints[m] > ints[m + 1]) { int tmp = ints[m];ints[m] = ints[m + 1];ints[m + 1] = tmp;//当发生交换时，将flag置为1flag = 1;}}}//检验结果for (int i = 0; i < sizeof(ints) / sizeof(ints[0]); i++) { printf("%d ", ints[i]);}}

Java

import java.util.Arrays;public class Main { public static void main(String[] args) { int[] ints = { 5, 2, 4, 3};//标记完成状态boolean flag = true;//比较n-1趟for (int i = 0; i < ints.length - 1 && flag; i++) { //将标记置为0flag = false;//每趟比较n-1次for (int m = 0; m < ints.length - 1 - i; m++) { //将较大值置于数组右侧if (ints[m] > ints[m + 1]) { int tmp = ints[m];ints[m] = ints[m + 1];ints[m + 1] = tmp;//当发生交换时，将flag置为1flag = true;}}}//检验结果System.out.println(Arrays.toString(ints));}}

需要注意的是，内层循环的结束条件与m无关。

选择排序

分别从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。选择排序是不稳定的排序算法，即对于值相同的数据元素，彼此的前后顺序可能会发生改变。

对比冒泡排序

与冒泡排序不同：

• 冒泡排序是逐趟选出未排序序列中的最大值，置于右侧。
• 选择排序是逐趟选出未排序序列中的最小值，置于左侧。
• 冒泡排序会两两比较相邻元素，将较大值通过多次交换移动到数列右侧，第i趟最多交换n-i次。
• 选择排序会通过多次比较记录最小元素的下标，在这一趟结束时才发生交换，每趟最多交换1次。

即重复这两个步骤：

1. 遍历无序序列，记录无序数列的最小值的下标。
2. 将下标对应的元素与无序数列的最左端元素交换位置。

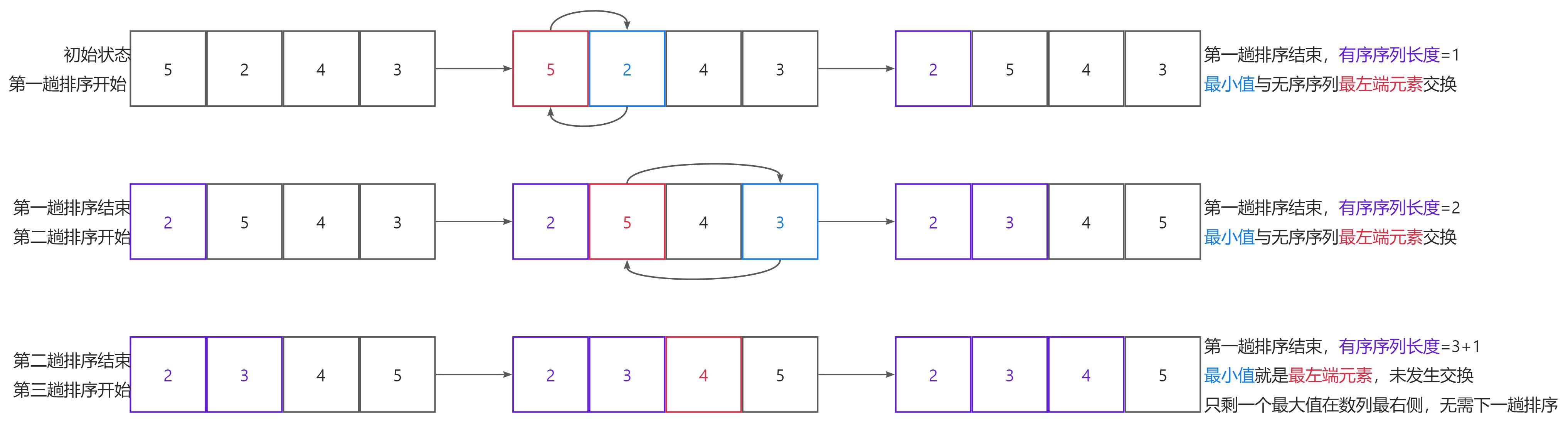
代码如下：

Java

import java.util.Arrays;public class Main { public static void main(String[] args) { int[] ints = { 5, 2, 4, 3};//用于记录最小值的下标int minIndex = 0;//控制轮数for (int i = 0; i < ints.length - 1; i++) { minIndex = i;//在未排序的子序列中找到最小元素的位置for (int j = i + 1; j < ints.length; j++) { if (ints[j] < ints[minIndex]) { //用minIndex记录最小元素的位置minIndex = j;}}//交换元素，将较小值置于左侧if (minIndex != i) { int tmp = ints[minIndex];ints[minIndex] = ints[i];ints[i] = tmp;}}//检验结果System.out.println(Arrays.toString(ints));}}

C/C++

#includeint  main() { int ints[] = {  5,2,4,3 };//标记最小值下标char minIndex = 0;//比较n-1趟for (int i = 0; i < sizeof(ints) / sizeof(ints[0]) - 1; i++) { minIndex = i;for (int m = i + 1; m < sizeof(ints) / sizeof(ints[0]); m++) { if (ints[m] < ints[minIndex]) { minIndex = m;}}//交换元素，将较小值置于左侧if (minIndex != i) { int tmp = ints[i];ints[i] = ints[minIndex];ints[minIndex] = tmp;}}//检验结果for (int i = 0; i < sizeof(ints) / sizeof(ints[0]); i++) { printf("%d ", ints[i]);}}

需要注意：

• 对于n个元素，需要排序的趟数仍然是n-1。
• 不同于冒泡排序，选择排序每趟排序最多只会改变两个元素的位置。不能设置flag检查是否排序完成，也无法通过flag检查。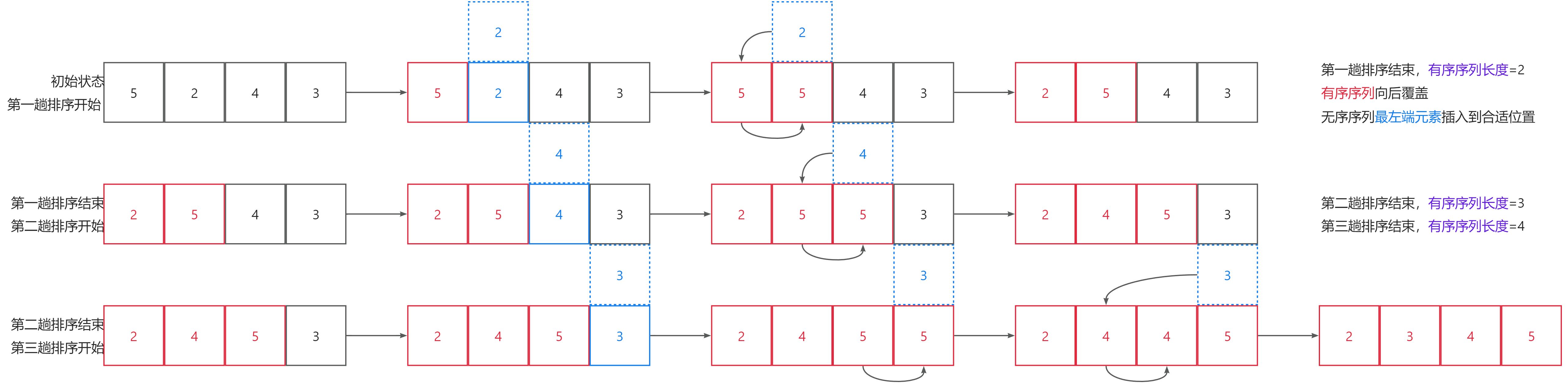
• 选择排序需要遍历剩余所有元素，内层循环不能同冒泡循环一样修改右边界。并且要保证能访问到数列的最后一个元素。

  插入排序

  逐步将无序序列中的元素，插入到前面已排好的有序序列的合适位置。
   

  C/C++

#includeint  main() { int ints[] = {  5,2,4,3 };//遍历数列for (int i = 1; i < sizeof(ints) / sizeof(ints[0]); i++) { //定义临时变量存储当前序列取出的值int tmp = ints[i];int j = 0;//寻找合适位置for (j = i - 1; j >= 0; j--) { //需要移动的数据向后覆盖if (ints[j] > tmp) { ints[j + 1] = ints[j];}else break;}if (ints[j + 1] != tmp) { ints[j + 1] = tmp;}}//检验结果for (int i = 0; i < sizeof(ints) / sizeof(ints[0]); i++) { printf("%d ", ints[i]);}}

Java

import java.util.Arrays;public class Main { public static void main(String[] args) { int[] ints = { 5, 2, 4, 3};//遍历数列for (int i = 1; i < ints.length; i++) { //定义临时变量存储当前序列取出的值int tmp = ints[i];int j = 0;//寻找合适位置for (j = i - 1; j >= 0 && ints[j] > tmp; j--) { ints[j + 1] = ints[j];}//插入到合适位置if (ints[j + 1] != tmp) { ints[j + 1] = tmp;}}//检验结果System.out.println(Arrays.toString(ints));}}

要点如下：

• 如果数据结构是数组，那么每次插入都需要将插入位置以后的元素向后移动，移动元素会覆盖该元素的下一个元素。会导致ints[i]被覆盖，因此必须要使用临时变量tmp存储每趟排序中的ints[i]的值。
• 我们需要对数组的每个元素都进行遍历，以保证每个元素都被取出并插入到合适位置。因此外重循环的结束条件为元素个数n而不是n-1。
• 在第一趟插入中，我们将原数列的第1个元素取出作为有序数列，将第2个元素取出作为新元素插入，对应的下标从1开始。虽然结束条件是n，外重循环的次数仍然是n-1。

• 在插入元素时，已经内层循环的结束条件，此时j小于零，或者已经指向合适位置的前一个位置。因此需要对ints[j+1]进行赋值，而非ints[j]。

  补充

  交换两个变量的值，除了可以使用第三个变量tmp，也可以使用加减法的方式处理，仅适用于数字类型。

  ints[m] = ints[m] + ints[n];ints[n] = ints[m] - ints[n];ints[m] = ints[m] - ints[n];

  总结

  三种排序方法每趟都只能确保一个数据加入有序数列后仍有序，外层循环执行的趟数都为n-1，n即元素个数。但由于计数器开始位置不同，可能为0，也可能为1，或者其它计数方式，不需要死记硬背，只需要保证能执行n-1趟即可。
  对于内层循环，还是由于三种排序方法每趟都只能确保一个数据加入有序数列后仍有序。有序序列每趟排序后长度都在增加，我们不需要对有序序列的元素再取出排序。我们只需要保证能遍历到无序序列中的每一个元素即可。

• 对于冒泡排序，有序序列默认在右端，左侧为无序序列，我们采取的方式是调整右边界。而内层循环每次从0开始，是为了能够遍历到左侧的无序序列的每一个元素。

• 对于选择排序，有序序列默认在左端，右侧为无序序列，我们采取的方式是调整左边界。内层循环的计数器初始值随趟数改变而改变，是为了保证每趟都指向无序序列的第一个元素，并能够遍历无序序列的每一个元素。
• 对于插入排序，有序序列默认在左端，我们需要取出无序序列中的元素之后遍历有序序列，寻找合适位置。由于有序序列是有序的，我们可以选择一个方向，寻找介于两个元素之间的位置插入。在有序序列寻找合适位置时需要考虑数组边界。

对于临时变量的定义，编译器可能存在零优化，如果定义在循环内部，那么可能出现频繁的创建和释放，提高占用时间。并且在插入排序中，如果数据结构是数组，那么数据的移动方式就是向后覆盖，可能导致无序数列的最左端元素被覆盖，我们需要使用临时变量提前保存数据。上面的代码中，为了便于理解，并没有将所有循环内的变量在循环内定义。但出于以上两点原因，建议将变量在循环外定义，在循环内使用。