前言

上一篇文章传送门

我们讲解了如何根据前序遍历构建 二叉树 ,以及 二叉树 的三种遍历(前、中、后序遍历)方法.

本文主要讲解对 二叉树 的几个节基本操作.

一、计算二叉树的结点个数

对于一棵 二叉树 ,如何计算它又多少个结点?

打工人篇:

遍历 二叉树 ,一个个数结点个数

创建一个变量count进行记录,然后遍历 二叉树 进行计数吗?那count变量创建在哪里呢?

方法一:

如果创建在函数内部,那么在递归过程中都会创建这个变量.这样累加结果不会保留.

方法二:如果是全局变量,可以实现在每次递归过程中累加的效果,但是进行第二次计算时,全局变量需要清零重新计算,否则会继续累加.全局变量终究是不妥当安全的.

领导篇: (分治法)让下属去做事

我们可以将一棵 二叉树 想象为学校的组织结构,如果校长想要知道全校的人数,他会怎么办?

校长总不可能一个个去数吧.打工人才是那样滴,领导才不会.校长可以找院长,让院长汇报他们学院有多少人,院长找班导,班导找寝室长(打工人),最后网上层层汇报.

校长只需要关注院长,院长只需要关注班导,班导只需要关注寝室长就行了.

即 二叉树 的每个结点只需要知道其 左右子树 的结点个数就行.

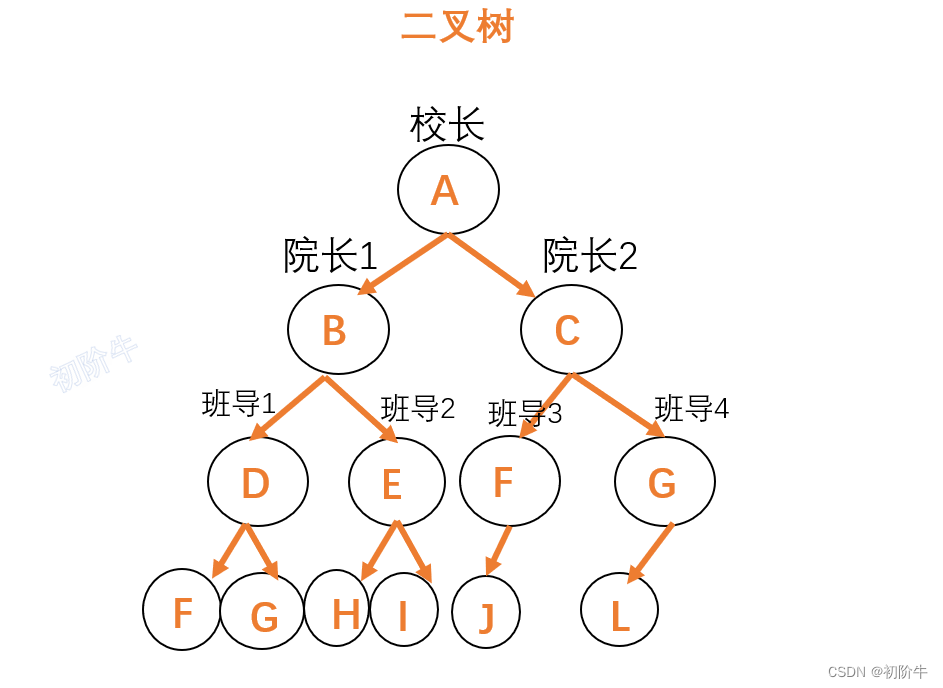
故 二叉树 的结点个数= 左子树+ 右子树 +1(自己本身).

代码实现:

// 二叉树节点个数 int BinaryTreeSize(BTNode* root) {  if (root == NULL)//遇到NULL返回0  {  return 0;  }  int left = BinaryTreeSize(root->left);//计算左子树的结点个数  int right = BinaryTreeSize(root->right);//计算右子树的结点个数  return left + right + 1;//左子树的结点个数+右子树的结点个数+自己本身 }

二、计算二叉树叶子结点个数.

提示: 二叉树 经常使用递归算法,不理解时可以画代码的递归展开图,一层层分析.更加方便理解

  叶子结点:度为0的节点称为叶节点

当一个结点的 左子树和 右子树都是NULL时,该结点便是叶子结点.

代码实现

// 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root) {  if (root == NULL)  {  return 0;  }  if (root->left == NULL && root->left == root->right)//判断是否是叶子结点  {  return 1;  }  int left = BinaryTreeLeafSize(root->left);//统计左子树中叶子结点的个数  int right = BinaryTreeLeafSize(root->right);//统计右子树中叶子结点的个数   return left + right; }

三、计算二叉树的高度

 如果校长需要知道全校最高的那个人,他只需要让院长去统计他们学院最高的那个人的身高,然后从院长报上来的身高中选出较大者即可.

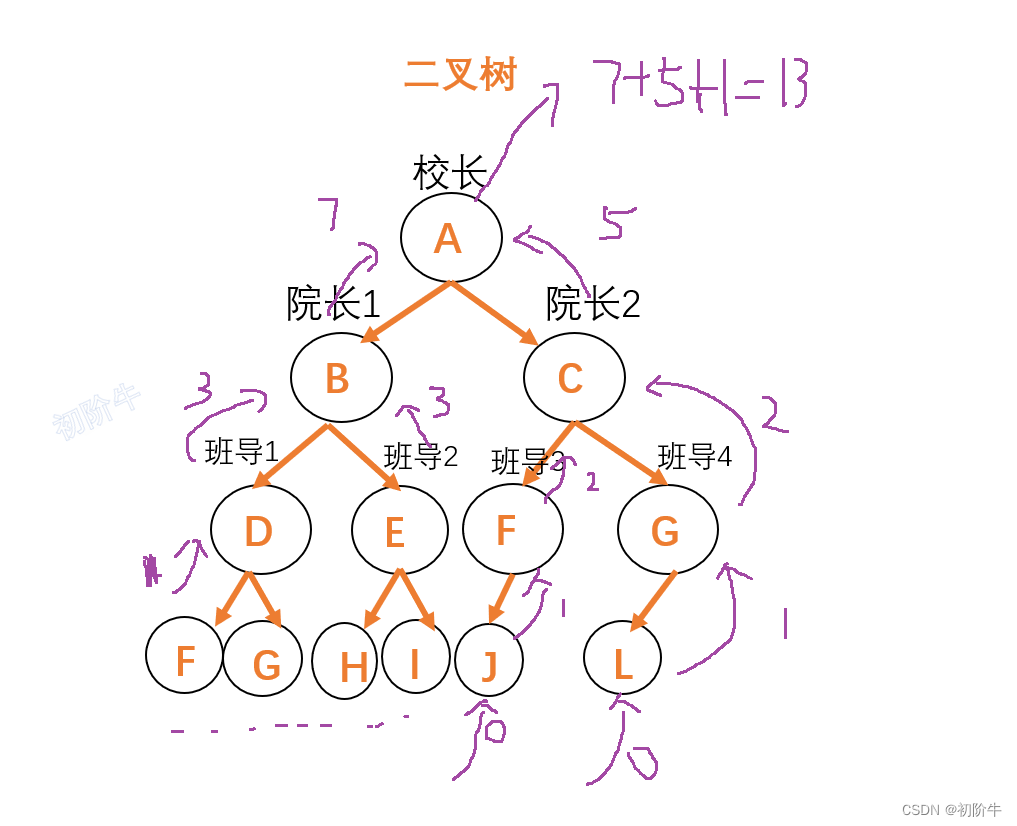
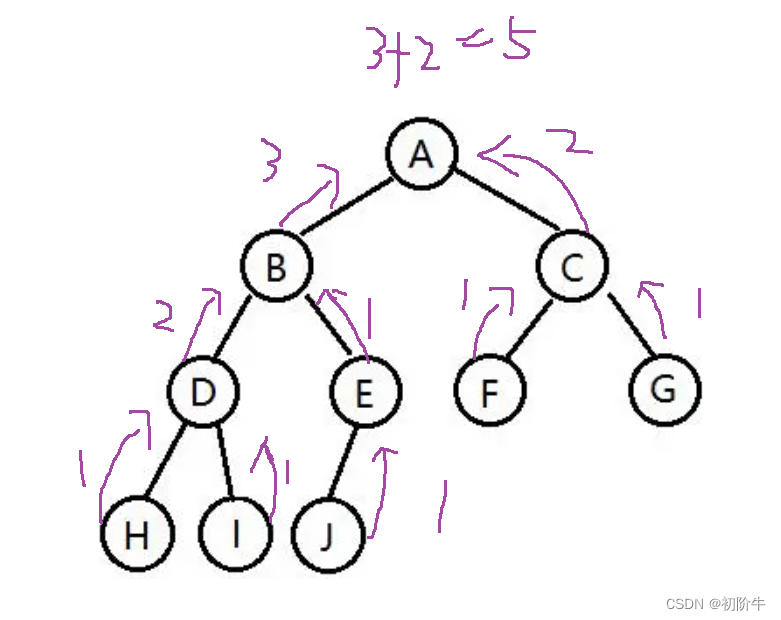
同样采用分治的方法,如果我们需要知道这颗树的高度,只需要计算它的左子树的高度,和右子树的高度,然后取较高的那个一棵,加上自己这一层的高度.

树的高度=max( 左子树的高度, 右子树的高度)+1(本身这一层).

代码1:

int TreeHeight(BTNode* root) {  if (root == NULL)  {  return 0;  }  //选出左右子树中的较大者  return TreeHeight(root->left) > TreeHeight(root->right)  ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1; }

这个代码看起来没有问题,但是效率极低,如果现实生活中校长这样做事,最难受的就是寝室长(最强打工人了).

 就好比是这样的,寝室长统计了寝室最高的人名单交给班主任,但是班主任它没有记录,他只知道A寝室的人最高,所以A寝室的寝室长又要报上去一遍,班主任这次知道具体身高了,往上报给院长,院长只知道是A导员班上的人最高,但是也没有记录具体数值,就又让A导员计算一遍,可气的是,A导员自己报上去之后,又没记录,又要找A寝室长汇报,如果这棵树的高度比较高的话,那么寝室长被叫的次数会很可怕.

第二层要被呼叫 2次

第三层要被呼叫 4次

第四层要被呼叫 8次

第五层要被呼叫 16次

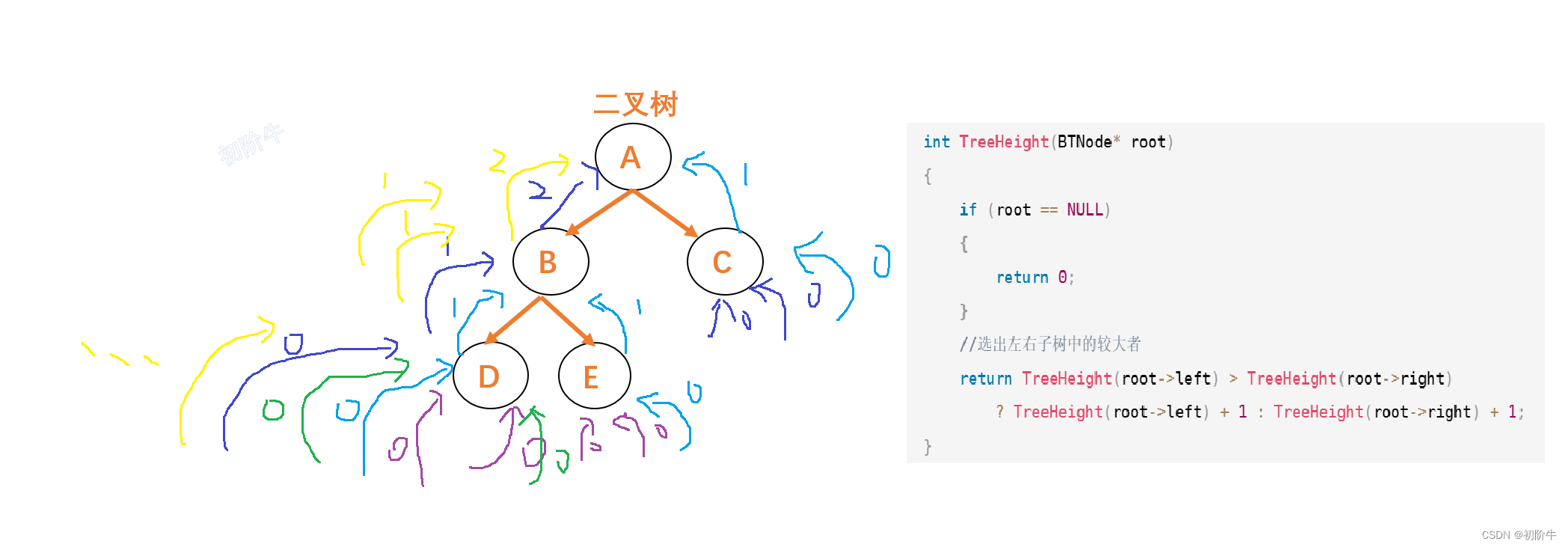
正确写法,将计算过的高度保存下来.

代码实现

//二叉树的高度 int TreeHeight(BTNode* root) {  if (root == NULL)  {  return 0;  }  int left = TreeHeight(root->left);//记录左子树的高度  int right = TreeHeight(root->right);//记录右子树的高度  return left > right ? left + 1 : right + 1; }

四、计算二叉树第k层结点的个数.

第 k 层的结点个数=第 k-1 层的 左子树结点个数+ 右子树结点个数.

代码实现

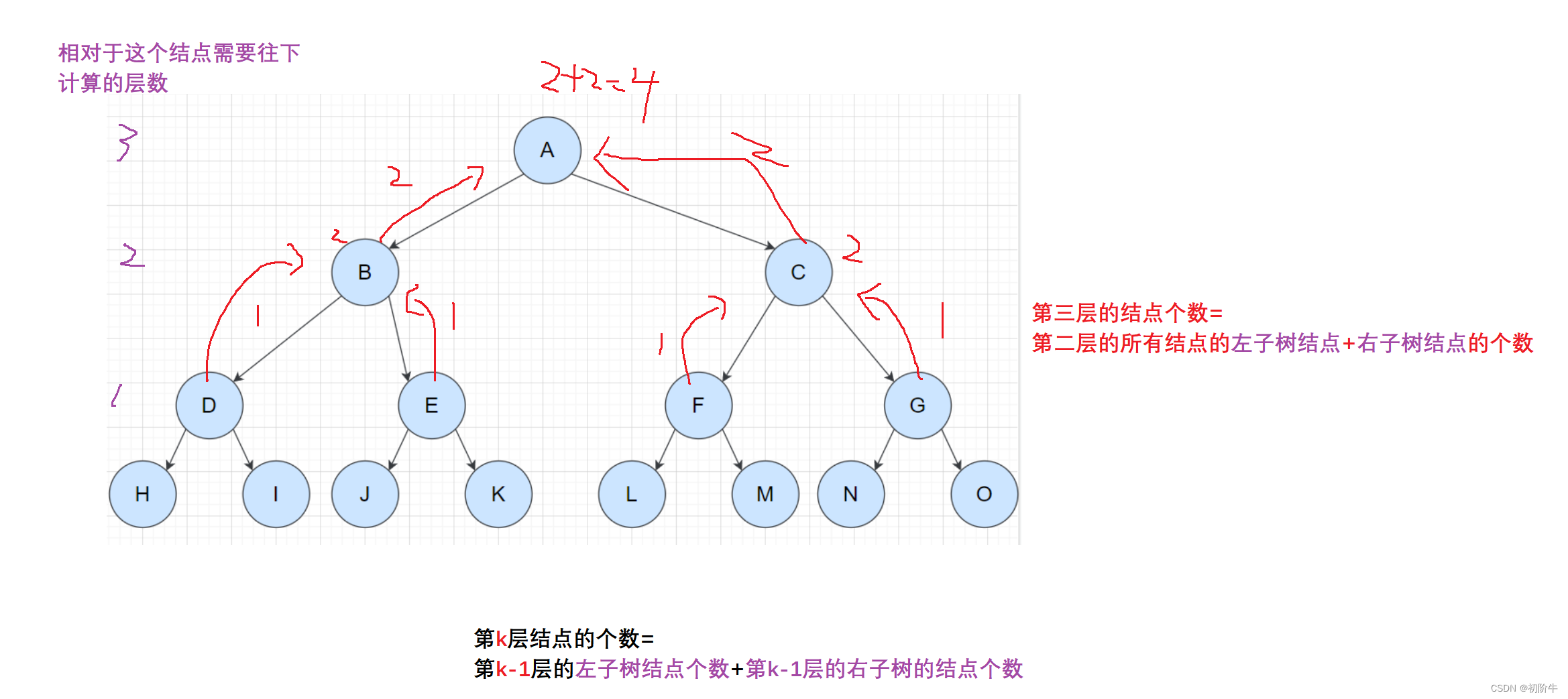
// 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k) {  if (root == NULL)  {  return 0;  }  if (k == 1)//表示就是要计算的这层的结点个数  {  return 1;  }  int left = BinaryTreeLevelKSize(root->left, k - 1);  int right = BinaryTreeLevelKSize(root->right, k - 1);  return left + right; }

五、查找二叉树中的目标值

在 二叉树 中寻找目标值,最需要注意的是返回值问题.

先判断根节点,根节点找到课

再搜索 左子树,如果 左子树找到了,则返回该结点.

左子树没有找到,再搜索 右子树,如果 右子树找到了,返回该结点

最后,如果 左右子树都没有找到,则返回NULL.

代码实现

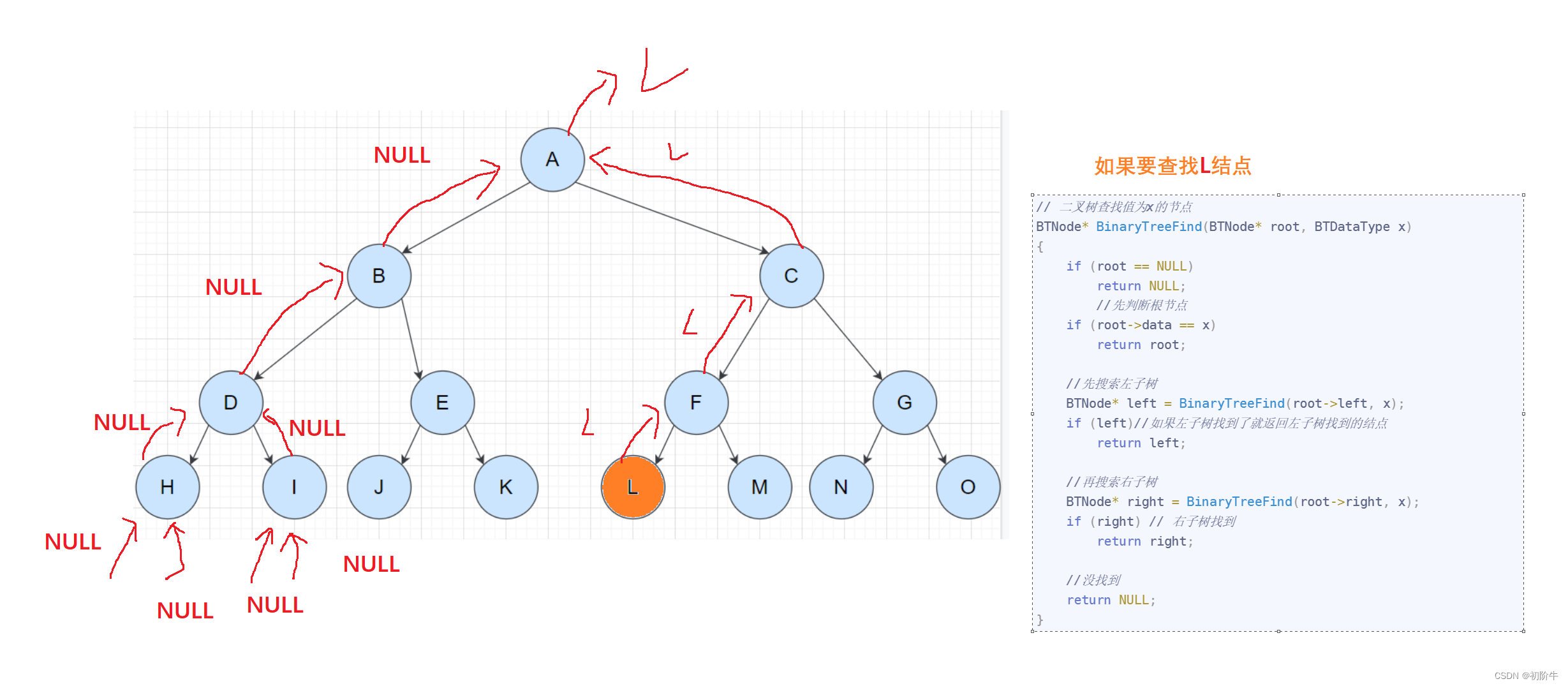
// 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {  if (root == NULL)  return NULL;  //先判断根节点  if (root->data == x)  return root;   //先搜索左子树  BTNode* left = BinaryTreeFind(root->left, x);  if (left)//如果左子树找到了就返回左子树找到的结点  return left;   //再搜索右子树  BTNode* right = BinaryTreeFind(root->right, x);  if (right) // 右子树找到  return right;   //没找到  return NULL; }

六、总代码

测试区

#include "tree.h" int main() {  //BTDataType arr[50] = { "ABD##E##CF##G##" };  BTDataType arr[50] = { "ABD##E##CF##GH###" };  int i = 0;  BTNode* root = BinaryTreeCreate(arr, &i);   // 二叉树节点个数  printf("二叉树结点的个数是:");  printf("%d", BinaryTreeSize(root));  printf("\n");   // 二叉树叶子节点个数  printf("二叉树叶子结点的个数是:");  printf("%d", BinaryTreeLeafSize(root));  printf("\n");    //二叉树第k层节点个数  printf("二叉树第3层节点个数是:");  printf("%d", BinaryTreeLevelKSize(root, 3));  printf("\n");   //二叉树第k层节点个数  printf("二叉树高度是:");  printf("%d", TreeHeight(root));  printf("\n");   // 二叉树查找值为x的节点  BTNode* ret = BinaryTreeFind(root, 'H');  if (ret)  {  printf("找到了该结点:%c", ret->data);  }  else  {  printf("没有找到该结点.\n");  }   BinaryTreeDestory(root);   return 0; }

接口实现区

 #include "tree.h"  //根据前序遍历构建二叉树 BTNode* BinaryTreeCreate(BTDataType* a, int* pi)//pi用于遍历这个数组 {  //递归的结束条件是,当left和right都是NULL时  if (a[*pi] == '#')//遇到NULL  {  (*pi)++;  return NULL;  }  //如果不是NULL  BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建树结点  root->data = a[(*pi)++];  root->left = BinaryTreeCreate(a, pi);  root->right = BinaryTreeCreate(a, pi);  return root; }    //二叉树的销毁 void BinaryTreeDestory(BTNode* root) {  if (root == NULL)//如果走到NULL则直接返回  {  return;  }  BinaryTreeDestory(root->left);  BinaryTreeDestory(root->right);  free(root);//这条语句一定要放在前面两条语句的后面,不然无法递归往下走. }   // 二叉树节点个数 int BinaryTreeSize(BTNode* root) {  if (root == NULL)  {  return 0;  }  int left = BinaryTreeSize(root->left);  int right = BinaryTreeSize(root->right);  return left + right + 1;//左子树的结点个数+右子树的结点个数+自己本身 }   // 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root) {  if (root == NULL)  {  return 0;  }  if (root->left == NULL && root->left == root->right)  {  return 1;  }  int left = BinaryTreeLeafSize(root->left);  int right = BinaryTreeLeafSize(root->right);  return left + right; }  //二叉树的高度 //int TreeHeight(BTNode* root) //{ // if (root == NULL) // { // return 0; // } // int left = TreeHeight(root->left); // int right = TreeHeight(root->right); // return left > right ? left + 1 : right + 1; //}  int TreeHeight(BTNode* root) {  if (root == NULL)  {  return 0;  }  return TreeHeight(root->left) > TreeHeight(root->right)  ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1; }   // 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k) {  if (root == NULL)  {  return 0;  }  if (k == 1)  {  return 1;  }  int left = BinaryTreeLevelKSize(root->left, k - 1);  int right = BinaryTreeLevelKSize(root->right, k - 1);  return left + right; }   // 二叉树查找值为x的节点  BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {  if (root == NULL)  return NULL;  if (root->data == x)  return root;   //先搜索左子树  BTNode* left = BinaryTreeFind(root->left, x);  if (left)//如果左子树找到了就返回左子树找到的结点  return left;   //再搜索右子树  BTNode* right = BinaryTreeFind(root->right, x);  if (right) // 右子树找到  return right;   //没找到  return NULL; }

声明区

#include#include#include typedef char BTDataType;   typedef struct BinaryTreeNode {  BTDataType data;  struct BinaryTreeNode* left;  struct BinaryTreeNode* right; }BTNode;  //根据前序遍历构建二叉树 BTNode* BinaryTreeCreate(BTDataType* a, int* pi);  // 二叉树销毁 void BinaryTreeDestory(BTNode* root);  // 二叉树节点个数 int BinaryTreeSize(BTNode* root);  // 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root);  //二叉树的高度 int TreeHeight(BTNode* root);   // 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k);  // 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, BTDataType x);