前言

前面,我们在"树的概念"一文中已经介绍过了二叉树的基本概念,二叉树较于线性表(顺序表和链表等),难度有一定提升,主要是要熟练掌握递归,很多有关"二叉树"的操作都需要使用递归算法.

一、"二叉树"的类型声明

typedef char BTDataType;  typedef struct BinaryTreeNode {  BTDataType data;//数据域  //指针域  struct BinaryTreeNode* left;//左子树  struct BinaryTreeNode* right;//右子树 }BTNode;

二、"二叉树"的遍历

学习二叉树的结构时，最简单的操作是遍历二叉树,所以我们先介绍如何遍历一课二叉树.

二叉树遍历(Traversal):

按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

通俗来讲,就是访问一遍二叉树的所有结点.

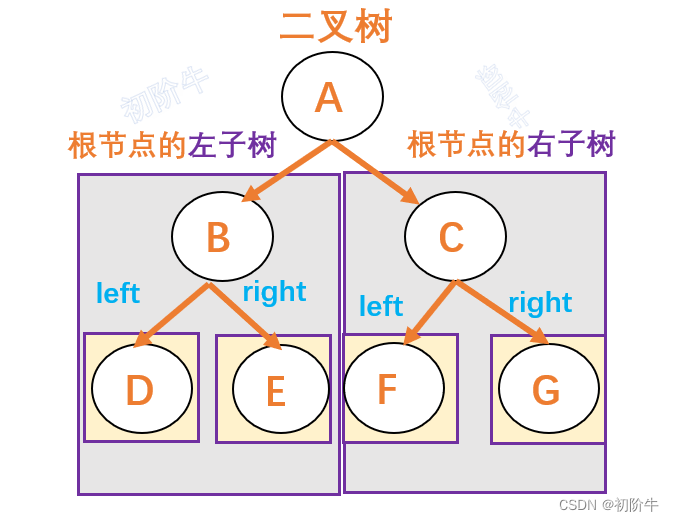
对于任意一棵二叉树,他都有由根,左子树,右子树组成.

那么就出现了三种常见的遍历二叉树的方式

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。即:

根 ---> 左(子树) ---> 右(子树)

1. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。即:

左(子树) ---> 根 ---> 右(右子树)

1. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。即:

左(子树) ---> 右(子树) ---> 根

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历.

总结:

在 根 左子树 右子树三个中:

前序遍历:根节点第一个被访问.

中序遍历:根节点第中间(二个)个被访问.

后序遍历:根节点最后一个被访问.

2.1 前序遍历:

看见前序遍历,就知道根节点是第一个被访问的.即:

根 —> 左(子树) —> 右(子树)

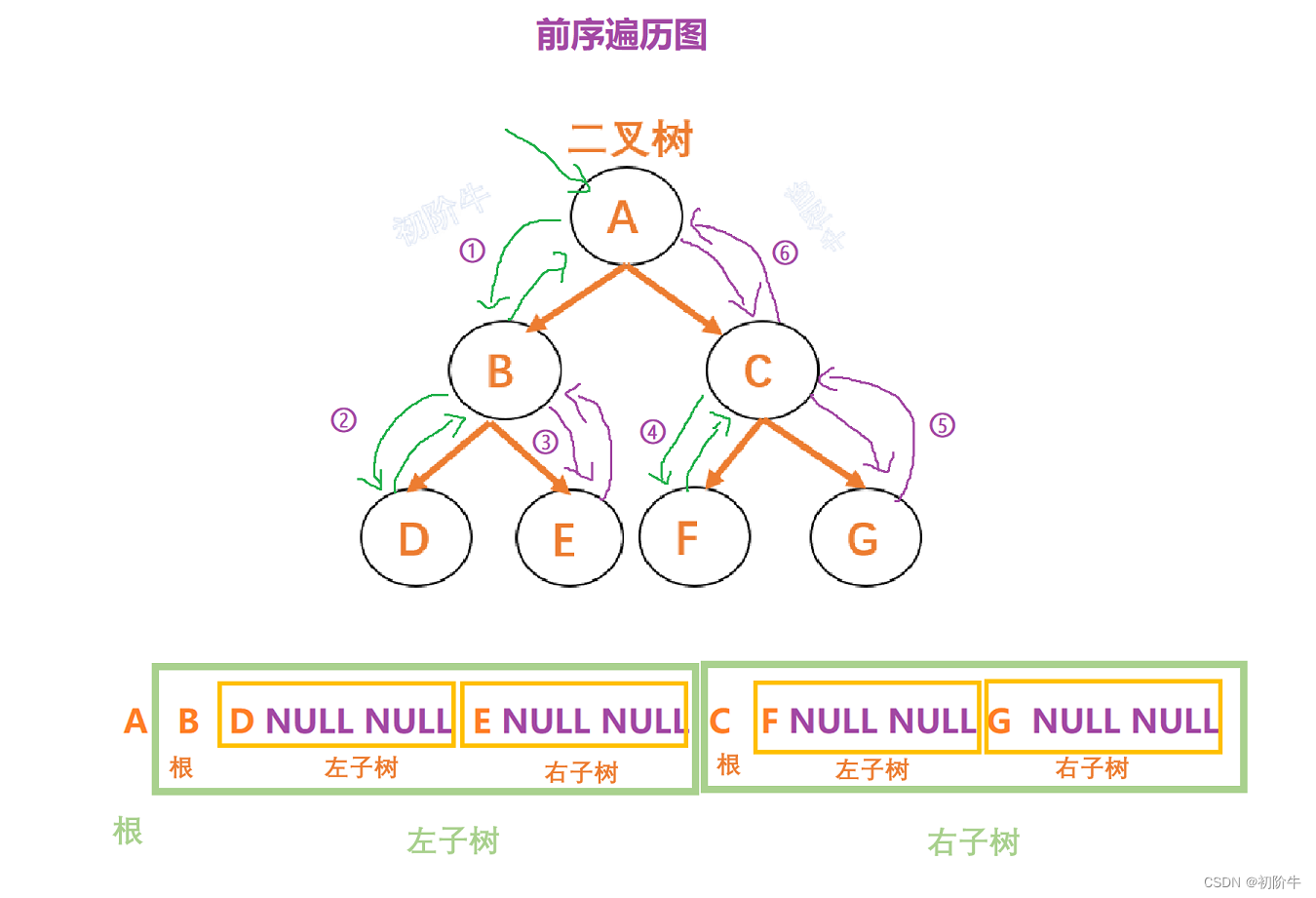
代码递归展开图:

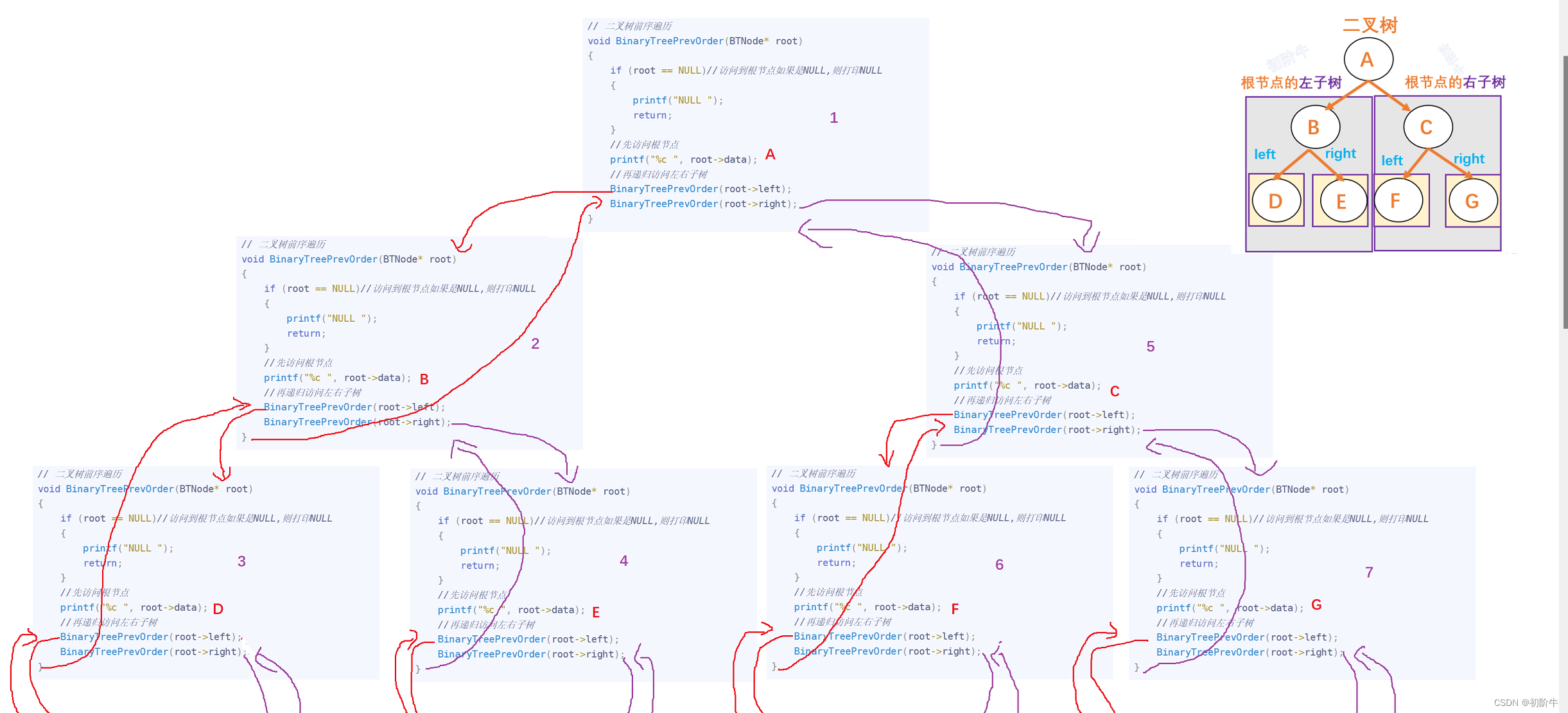
代码实现:

// 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) {  if (root == NULL)//访问到根节点如果是NULL,则打印NULL  {  printf("NULL ");  return;  }  //先访问根节点  printf("%c ", root->data);  //再递归访问左右子树  BinaryTreePrevOrder(root->left);  BinaryTreePrevOrder(root->right); }

2.2 中序遍历:

有了前序遍历的基础,后面两个应该好理解,如果还是不理解,可以试着画一下代码的递归展开图,帮助大家理解.

// 二叉树中序遍历 void BinaryTreeInOrder(BTNode* root) {  if (root == NULL)  {  printf("NULL ");  return;  }  //先访问左子树  BinaryTreePrevOrder(root->left);  //中间访问根节点  printf("%c ", root->data);  //最后访问右子树  BinaryTreePrevOrder(root->right); }

2.3 后序遍历:

// 二叉树后序遍历 void BinaryTreePostOrder(BTNode* root) {  if (root == NULL)  {  printf("NULL ");  return;  }  //先访问左右子树  BinaryTreePrevOrder(root->left);  BinaryTreePrevOrder(root->right);  //最后访问根节点  printf("%c ", root->data); }

2.4 扩展知识:层序遍历(稍复杂)

要去按层来访问二叉树.

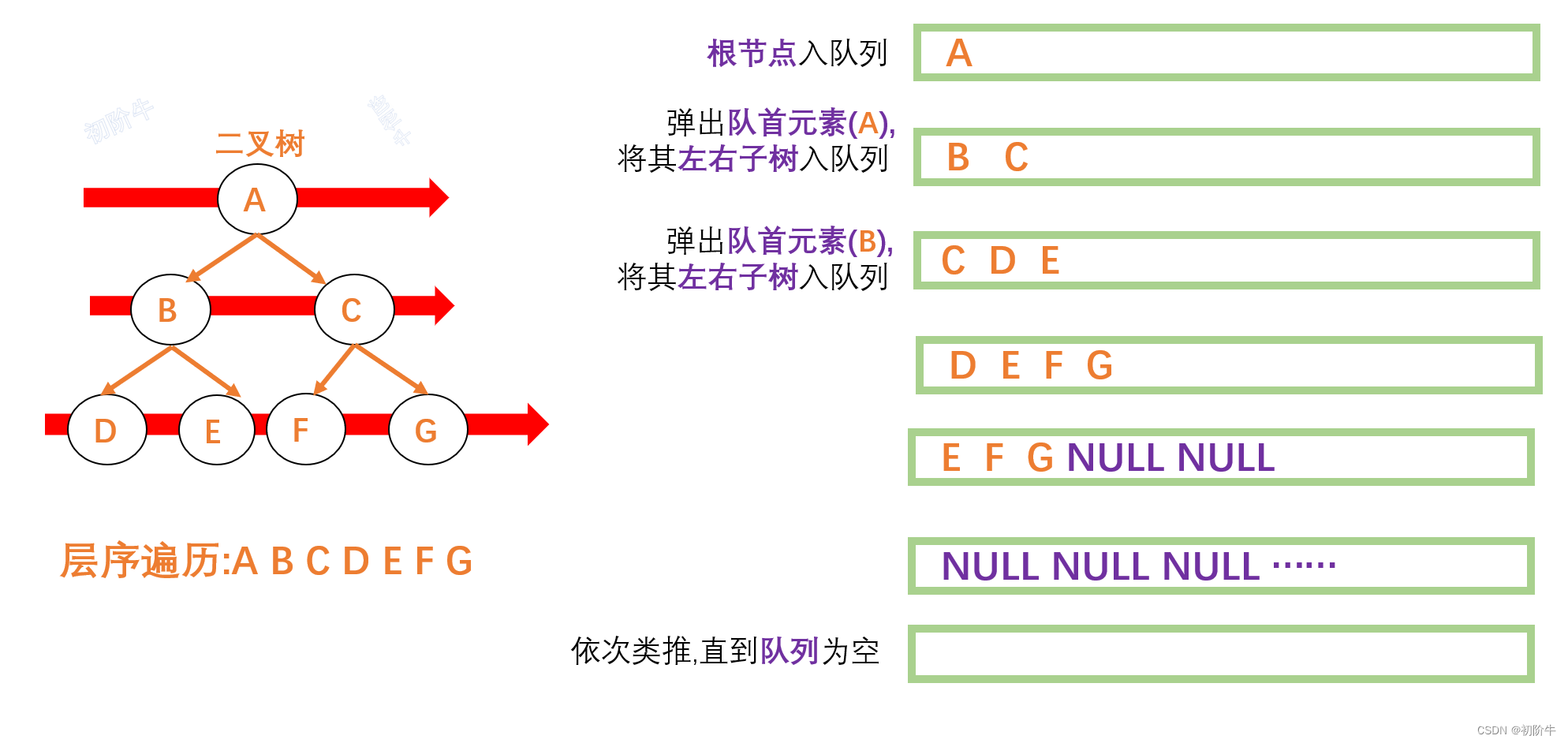
这里需要借助队列来实现,而且恶心的是, C语言没有队列的库函数,需要自己实现.

牛牛有关队列的博客,欢迎直接复制.

传送门

代码实现:

打印NULL版本

// 层序遍历 void BinaryTreeLevelOrder(BTNode* root) {  Queue q;  QueueInit(&q);  QueuePush(&q, root);//将二叉树的根节点先入队列  while (!QueueEmpty(&q))//只要队列非空则,继续  {  BTNode* tmp=QueueFront(&q);  if (tmp)//非空结点则直接打印数据  {  printf("%c ", tmp->data);  }  else  {  printf("NULL ");  }  QueuePop(&q);//弹出根节点.将左右子树分别压入队列  if (tmp)//只要该结点不是NULL,则将其左右子树都入队  {  //结点虽然非空,但是左右子树可能是NULL,所以这里NULL也进入队列了.  QueuePush(&q, tmp->left);  QueuePush(&q, tmp->right);  }  } }

不打印NULL版本

// 层序遍历 void BinaryTreeLevelOrder(BTNode* root) {  Queue q1;  QueueInit(&q1);  QueuePush(&q1, root);//将根节点存入队列  while (!QueueEmpty(&q1))  {  BTNode* front = QueueFront(&q1);//保存队首结点  printf("%c ",front->data );//打印队首数据  QueuePop(&q1);//弹出根节点  //将刚刚弹出的结点的左右孩子入队列(所以前面要保存头结点)  if (front->left)  QueuePush(&q1, front->left);  if(front->right)  QueuePush(&q1,front->right);  } }

三、"二叉树"的构造(根据前序遍历)

前面都是在已经有二叉树的基础上,我们直接遍历二叉树,那二叉树怎么构建呢?

现在,我们给出要构建的二叉树的前序遍历.(#代表NULL)

BTDataType arr[50] = { "ABD##E##CF##G##" };

代码实现:

BTNode* BinaryTreeCreate(BTDataType* a,int* pi)//pi用于遍历这个数组 {  //递归的结束条件是,当left和right都是NULL时,(左右子树都为空,则结束递归)  if (a[*pi] == '#')//遇到NULL  {  //注意,即使是遇到NULL,数组也需要继续往后遍历,不然还没有构建完成  (*pi)++;  return NULL;  }  //如果不是NULL  BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建树结点  //先赋值根节点  root->data = a[(*pi)++];  //再给左右子树赋值  root->left = BinaryTreeCreate(a, pi);  root->right = BinaryTreeCreate(a,pi);  return root; }

四、"二叉树"的销毁

二叉树的销毁步骤:

1. 递归访问左右子树,直到遇到NULl.访问到了最后一层.

1. 开始释放该结点(从叶子结点开始),回退.

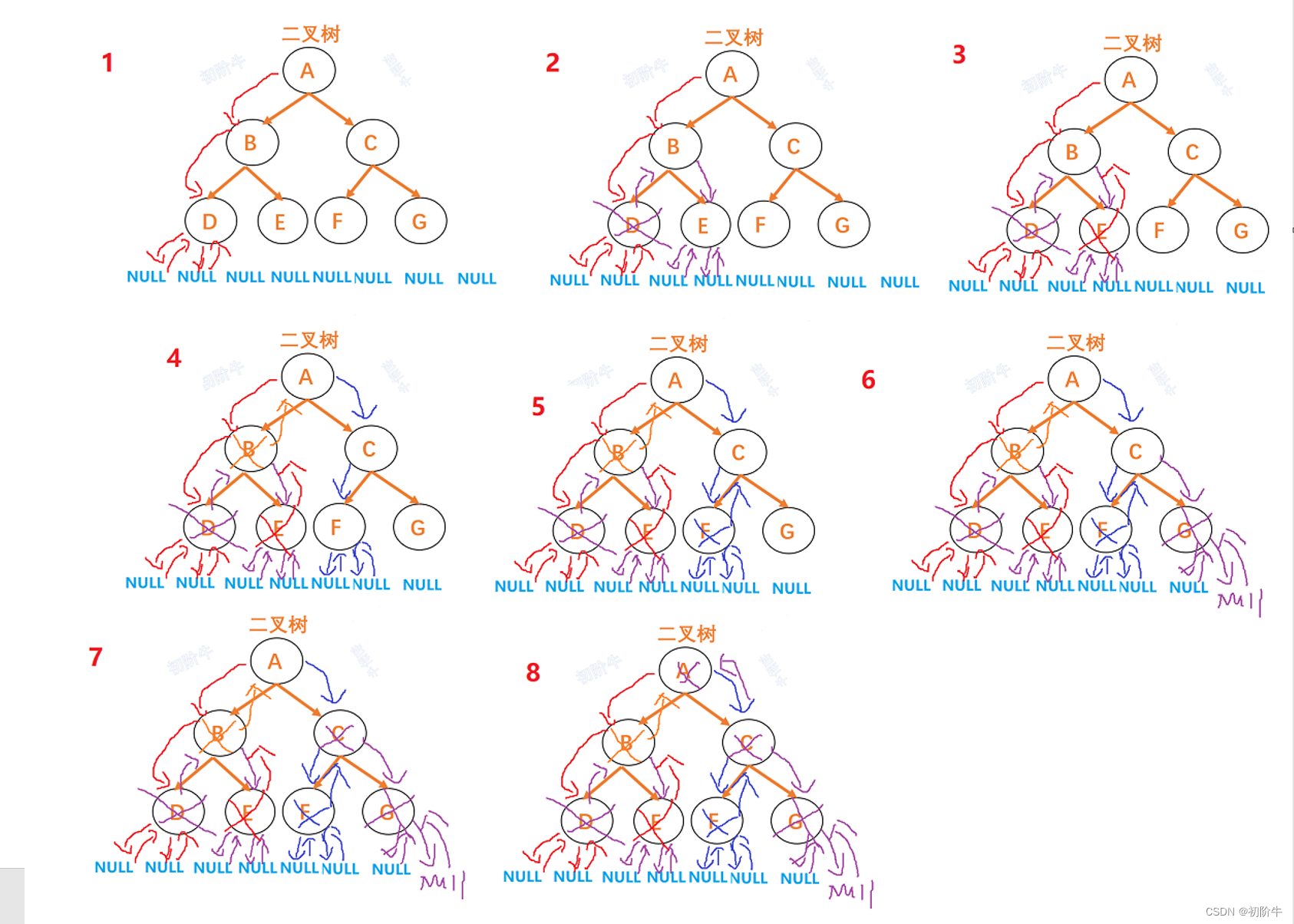
//二叉树的销毁 void BinaryTreeDestory(BTNode* root) {  if (root == NULL)//如果走到NULL则直接返回  {  return;  }  BinaryTreeDestory(root->left);  BinaryTreeDestory(root->right);  free(root);//这条语句一定要放在前面两条语句的后面,不然无法递归往下走. }

五、总代码:

声明区(tree.h)

#pragma once #include#include#include typedef char BTDataType;   typedef struct BinaryTreeNode {  BTDataType data;  struct BinaryTreeNode* left;  struct BinaryTreeNode* right; }BTNode;  //根据前序遍历构建二叉树 BTNode* BinaryTreeCreate(BTDataType* a,int* pi);  // 二叉树销毁 void BinaryTreeDestory(BTNode* root);  // 二叉树节点个数 int BinaryTreeSize(BTNode* root);  // 二叉树叶子节点个数 int BinaryTreeLeafSize(BTNode* root);  // 二叉树第k层节点个数 int BinaryTreeLevelKSize(BTNode* root, int k);  // 二叉树查找值为x的节点 BTNode* BinaryTreeFind(BTNode* root, BTDataType x);  // 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root);  // 二叉树中序遍历 void BinaryTreeInOrder(BTNode* root);  // 二叉树后序遍历 void BinaryTreePostOrder(BTNode* root);  // 层序遍历 void BinaryTreeLevelOrder(BTNode* root);    //队列 #include#include#include#include typedef BTNode* QDatatype;  typedef struct QueueNode {  struct QueueNode* next;  QDatatype data; }QNode;  typedef struct Queue {  QNode* head;  QNode* tail;  int size; }Queue;  void QueueInit(Queue* pq); void QueueDestroy(Queue* pq); void QueuePush(Queue* pq, QDatatype x); void QueuePop(Queue* pq); int QueueSize(Queue* pq); bool QueueEmpty(Queue* pq); QDatatype QueueFront(Queue* pq); QDatatype QueueBack(Queue* pq);

队列接口实现区:(Queue.c)

#include "tree.h" void QueueInit(Queue* pq) {  assert(pq);  pq->head = pq->tail = NULL;  pq->size = 0; }  void QueueDestroy(Queue* pq) {  assert(pq);  QNode* cur = pq->head;  QNode* next = cur;  while (next)  {  next = cur->next;  free(cur);  cur = next;  }  pq->head = pq->tail = NULL;  pq->size = 0; }  void QueuePush(Queue* pq, QDatatype x) {  assert(pq);  QNode* newnode = (QNode*)malloc(sizeof(QNode));  newnode->data = x;  newnode->next = NULL;  if (newnode == NULL)  {  perror("newnode malloc fail:");  return;  }  //这里忘记了判断head刚开始时  if (pq->head == NULL)//第一次插入  {  assert(pq->tail == NULL);  pq->head = pq->tail = newnode;  }  else  {  pq->tail->next = newnode;  pq->tail = newnode;  }  pq->size++;//记住这个放后面 } bool QueueEmpty(Queue* pq) {  assert(pq);  if (pq->head == pq->tail && pq->head == NULL)  {  return true;  }  return false; } void QueuePop(Queue* pq) {  assert(pq);  assert(!QueueEmpty(pq));  if (pq->head->next == NULL)//代表还剩下一个结点  {  free(pq->head);//释放这个结点.  pq->head = pq->tail = NULL;  }  else  {  QNode* next = pq->head->next;  free(pq->head);  pq->head = next;  }  pq->size--; }  int QueueSize(Queue* pq) {  assert(pq);  return pq->size; } QDatatype QueueFront(Queue* pq) {  assert(pq);  assert(pq->head);  return pq->head->data; }  QDatatype QueueBack(Queue* pq) {  assert(pq);  assert(pq->head);  return pq->tail->data; }

"二叉树"接口实现区:(tree.c)

#include "tree.h"  BTNode* BinaryTreeCreate(BTDataType* a,int* pi)//pi用于遍历这个数组 {  //递归的结束条件是,当left和right都是NULL时  if (a[*pi] == '#')//遇到NULL  {  (*pi)++;  return NULL;  }  //如果不是NULL  BTNode* root = (BTNode*)malloc(sizeof(BTNode));//创建树结点  root->data = a[(*pi)++];  root->left = BinaryTreeCreate(a, pi);  root->right = BinaryTreeCreate(a,pi);  return root; }   //二叉树的销毁 void BinaryTreeDestory(BTNode* root) {  if (root == NULL)//如果走到NULL则直接返回  {  return;  }  BinaryTreeDestory(root->left);  BinaryTreeDestory(root->right);  free(root);//这条语句一定要放在前面两条语句的后面,不然无法递归往下走. }  // 二叉树前序遍历 void BinaryTreePrevOrder(BTNode* root) {  if (root == NULL)  {  printf("NULL ");  return;  }  printf("%c ", root->data);  BinaryTreePrevOrder(root->left);  BinaryTreePrevOrder(root->right); }   // 二叉树中序遍历 void BinaryTreeInOrder(BTNode* root) {  if (root == NULL)  {  printf("NULL ");  return;  }  BinaryTreePrevOrder(root->left);  printf("%c ", root->data);  BinaryTreePrevOrder(root->right); }  // 二叉树后序遍历 void BinaryTreePostOrder(BTNode* root) {  if (root == NULL)  {  printf("NULL ");  return;  }  BinaryTreePrevOrder(root->left);  BinaryTreePrevOrder(root->right);  printf("%c ", root->data); }   // 层序遍历 void BinaryTreeLevelOrder(BTNode* root) {  Queue q;  QueueInit(&q);  QueuePush(&q, root);//将二叉树的根节点先入队列  while (!QueueEmpty(&q))//只要队列非空则,继续  {  BTNode* tmp=QueueFront(&q);  if (tmp)  {  printf("%c ", tmp->data);  }  else  {  printf("NULL ");  }  QueuePop(&q);//弹出根节点.将左右子树分别压入队列  if (tmp)  {  QueuePush(&q, tmp->left);  QueuePush(&q, tmp->right);  }  } }

主测试区:(test.c)

#include "tree.h"  int main() {  BTDataType arr[50] = { "ABD##E##CF##G##" };  int i = 0;  BTNode* root = BinaryTreeCreate(arr,&i);   //前序遍历  printf("前序遍历:");  BinaryTreePrevOrder(root);  printf("\n");   // 二叉树中序遍历  printf("中序遍历:");  BinaryTreeInOrder(root);  printf("\n");   // 二叉树后序遍历  printf("后序遍历:");  BinaryTreePostOrder(root);  printf("\n");   //层序遍历  printf("二叉树的层序遍历:");  BinaryTreeLevelOrder(root);  printf("\n");   //二叉树的销毁  BinaryTreeDestory(root);  return 0; }