素数算法主要应用于计算科学，密码学和数论等领域。例如，在密码学中，素数算法用于生成密钥；在数论中，素数算法用于研究质数分布。素数算法的历史可以追溯到公元前300年左右的古希腊数学家，他们发现了素数的重要性。随着数学和计算机科学的发展，素数算法也在不断改进和提高。

素数算法，是指用于求出素数的算法。主要有以下几种算法：

1. 暴力法：从 2 开始，一个一个数字遍历，判断是否为素数。
2. 筛法：埃氏筛法和欧拉筛法是其中常用的两种算法。
3. 埃式筛法：对于每个合数，找到其最小的质因数并将其标记为合数，每次标记一个数时都会标记一些数，这样逐渐缩小了搜索的范围。
4. Miller-Rabin算法：是一种更快的随机算法，它可以快速判断一个数是否为质数。
5. AKS算法：是一种判定素数的算法，该算法是2002年由Manindra Agrawal，Neeraj Kayal和 Nitin Saxena所提出的。
   这些算法的时间复杂度和空间复杂度各不相同，根据实际应用场景选择合适的算法即可。

Sieve of Eratosthenes 筛法求素数算法代码：
public static List sieveOfEratosthenes(int n) {
boolean[] prime = new boolean[n + 1];
Arrays.fill(prime, true);
for (int p = 2; p p <= n; p++) {
if (prime[p] == true) {
for (int i = p 2; i <= n; i += p) {
prime[i] = false;
}
}
}
List primeNumbers = new ArrayList<>();
for (int i = 2; i <= n; i++) {
if (prime[i] == true) {
primeNumbers.add(i);
}
}
return primeNumbers;
}

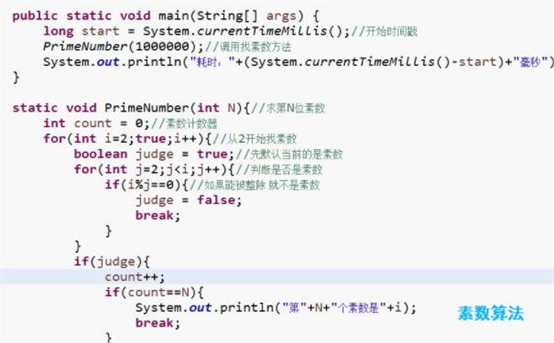
暴力法求素数算法代码：
public static boolean isPrime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i < n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}

本文转载自：https://www.vipshare.com/archives/40158